La peregrinación del caballo de ajedrez consiste en su paseo por todas las casillas del tablero
sin pasar dos veces por la misma, utilizando sus movimientos: dos casillas horizontales y una vertical o
a la inversa. Cuando desde la última casilla podamos pasar a la primera se trata de una "peregrinación cerrada".
A lo largo de los siglos, matemáticos de todo el mundo dedicaron un especial interés a este problema. Uno
de ellos se destacó por sus ingeniosas e increíbles soluciones, Leonard Euler (Basilea - Suiza, 1707-1783). Una
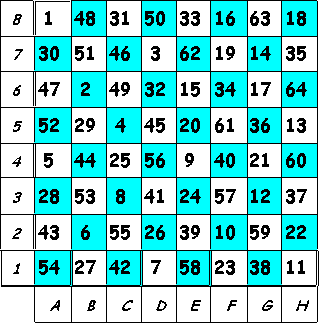
de sus soluciones es un recorrido en el que las filas y columnas suman 260. El desarrollo de los movimientos
del caballo por las 64 casillas ya es, en sí, muy difícil de conseguir como para, además, lograr que
filas y columnas sumen lo mismo.

Leonard Euler
Podemos imaginarnos cómo Euler, en el siglo XVIII, trabajó para resolver el acertijo, sus herramientas
fueron una pluma, papel, mucha paciencia y una grandísima dosis de algo que demostró toda su
vida: genialidad. Así, la técnica empleada sería, básicamente, la misma que he utilizado con ayuda de
un programa informático diseñado en B.A.S.I.C. para este estudio, realizar movimientos del caballo
de una a otra casilla hasta que, en el caso de que no queden casillas vacías, es necesario volver
atrás, borrar el movimiento anterior y realizar un salto de caballo distinto. El proceso se repite hasta
que se complete el recorrido.
A Euler le hubiera encantado disponer de la capacidad de cálculo de un ordenador. Al programa
en B.A.S.I.C., en cambio, me encantaría añadirle la genialidad que demostró este gran matemático. A
diferencia de los programas para jugar a ajedrez, este no da prioridad a los movimientos, el caballo puede
mover, como máximo, a ocho casillas y, como mínimo, a dos realizándose los ocho posibles movimientos
por orden. Así, intenta el primer movimiento, y si este no es posible porque la casilla está ocupada, intenta
el segundo y así, sucesivamente, hasta que completa todas las posibilidades.
Teniendo en cuenta que disponemos de 64 casillas y en cada movimiento de dos a ocho posibles
casillas para mover el caballo, podemos hacernos una idea del gran número de posibilidades. Sin entrar
en cálculos con grandes números, traducido a tiempo real, el algoritmo podría resultar “infinito”. Por
supuesto, se puede encontrar una solución en unos minutos o segundos si el ordenador realiza los
movimientos adecuados. Esto me indujo a pensar en realizar recorridos con menos casillas que se
pueden completar en pocos segundos, por ejemplo en un tablero de 4x4, de 5x5, de 3x8, etc,.
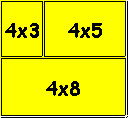
Para recorrer el tablero de ajedrez de 8x8 se pueden enlazar varios recorridos comenzando uno de
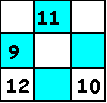
ellos en una casilla a la que se accede desde el último movimiento del anterior. Por ejemplo dos
recorridos de 3x3 se podrían enlazar como se muestra -desde la casilla de movimiento 8 pasamos
al siguiente con el movimiento 9-:
Aunque es posible acceder a la casilla que ha quedado vacía (movimiento 13), resulta más cómodo
buscar recorridos completos .
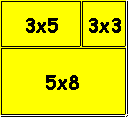
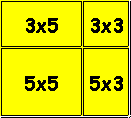
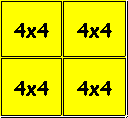
El siguiente paso es pensar de qué forma dividir el tablero en recorridos, por ejemplo:
Como es preferible que sean completos, hemos de analizar todas las posibilidades en cada uno
de ellos. A continuación se describen algunos recorridos completos y otros que no es posible
realizar (en estos se refleja un ejemplo, pero se han analizado todas las posibilidades):
3x3
 |
3x4
 |
3x5
 |
4x4
 |
| No hay solución |
|
No hay solución |
No hay solución |
4x5
 |
5x8
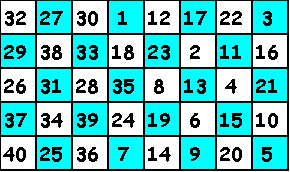 |
Una vez que tenemos claro qué recorridos son posibles, es necesario enlazarlos hasta
completar el tablero. Como ejemplo, el siguiente se ha realizado con uno de 8x5 y uno de 8x3. Dado
que desde la casilla número 64 se puede acceder a la número 1, se trata de un recorrido
cerrado que nos permite comenzar en cualquier casilla y siguiendo el orden de los números
completar el recorrido del caballo.
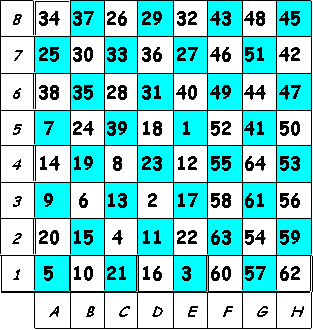
Por último, aquí está la increíble solución de EULER, en la que filas y columnas suman 260 (¡cuadrado mágico!).