Más artículos de Matemáticas
El Teorema de Wilson
Una prueba distinta



por Sebastián MARTÍN RUIZ

(Sebastián MARTÍN RUIZ es matemático y profesor en el Instituto de Educación Secundaria "Salmedina" de Chipiona, Cádiz-Spain)

En la mayoría de los libros de teoría de números el Teorema de Wilson es probado aplicando el Teorema de Lagrange para congruencias polinomiales [1,2,3,4]. Hardy & Wright también lo han probado usando residuos cuadráticos [3]. En este artículo el Teorema de Wilson se deriva como corolario de una identidad algebraica.

Teorema 1:

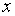Para todo entero y para todo número real se tiene:

Demostración:

Vamos a proceder por inducción. Sea

Es fácil comprobar que

Supongamos que R

Consideremos:

Separando el término y usando:

Tenemos:

= donde

==

Por tanto es constante, en particular:

Ya que el término es cero.


=

con lo cual hemos probado que y por inducción tenemos R N

Corolario 1: (Teorema de Wilson)

Para todo número primo , tenemos: .

Demostración:

Sea donde es primo. Usamos la fórmula para

(1)

Pero tenemos para :

De donde se deduce:

Usando este resultado en (1) obtenemos:

Si es impar y por tanto es par. Por ello tenemos la relación que usamos para obtener:

(2)

Por otro lado como es primo con podemos usar el Teorema de Fermat para obtener:

(3)

Combinamos (2) y (3), para concluir que:

y esta última relación puede ser escrita en la forma:

Corolario 2:

Para todo entero y para todo número real, se tiene:

Prueba:

Consideramos la identidad algebraica del teorema 1

Derivando j veces

Por tanto:

Referencias:

1: T.M. Apostol, Introduction to analytic number theory, Springer-Verlag, New York (1976)
2: R. D. Carmichael, Theory of Numbers, John Wiley and Sons, New York (1914)
3: G. H. Hardy and E. M. Wright, An introduction to the theory of numbers, Fourth edition, Oxford University Press (1960)
4: Kenneth Ireland and Michael Rosen, A classical introduction to modern number theory, second edition, Springer-Verlag, New York (1990)

Sebastián MARTÍN RUIZ
s_m_ruiz@yahoo.es
26 marzo 2005

 

Más artículos de Matemáticas