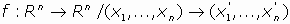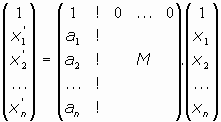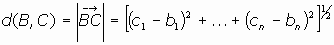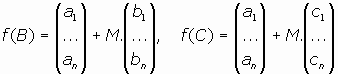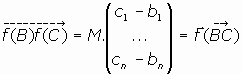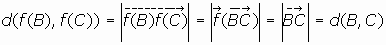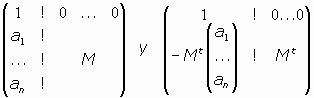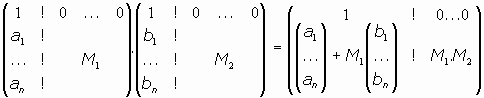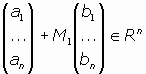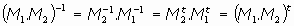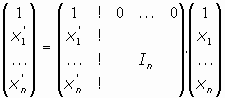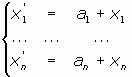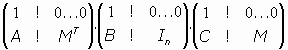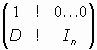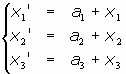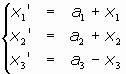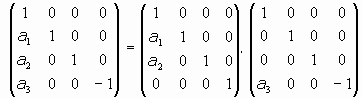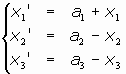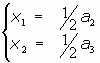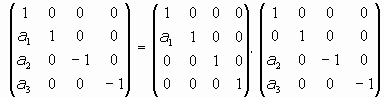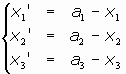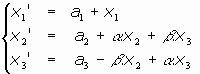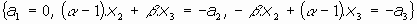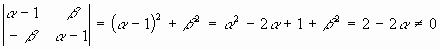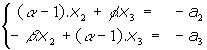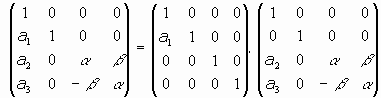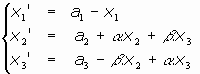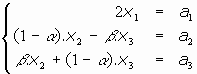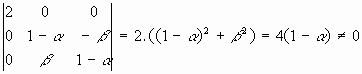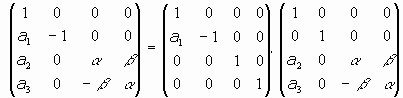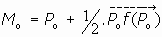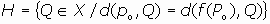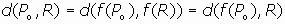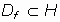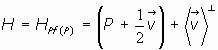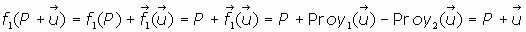¿De cuantas maneras podemos descomponer un movimiento en un espacio euclideo n-dimensional?. Esta es la interesante cuestión que resuelve uno de los grandes teoremas de la Geometría. Veremos que el maximo del número mínimo de simetrias especulares en las que un movimiento puede descomponerse depende del número de dimensiones del espacio.

En Geometría Analítica se estudian los MOVIMIENTOS en Rⁿ, que son funciones en Rⁿ como Espacio Afín Euclideo.

definidas por relaciones del tipo matricial siguiente:

donde , y M es una matriz ortogonal de orden nxn, es decir, que se verifica que M^-1 = M^t.

CONSECUENCIA 1ª:

Se tiene que los movimientos conservan las distancias entre puntos y, recíprocamente i.e., toda función de Rⁿ en sí mismo que conserve las distancias es un movimiento.

De hecho, podemos considerar a Rⁿ como un R-espacio vectorial y a la aplicación x'^t = M.x^t como una aplicación lineal que normalmente se denota por , y al ser M ortogonal son isometrías (conservan el producto escalar). Así con el producto escalar canónico podemos tomar dos puntos cualesquiera B(b₁,...,b₁) y C(c₁,...,c₁), la distancia entre ellos será:

donde es el vector de origen B y extremo C.

Como es

tenemos que

Por tanto:

puesto que es una isometría.

CONSECUENCIA 2ª:

Los movimientos de Rⁿ se denotan normalmente por Mov(Rⁿ) y constituyen un GRUPO.

Para ello observamos que la identidad, I_d, es evidentemente un movimiento, con matriz del tipo

donde I_n es la matriz identidad.

Además, la composición de un movimiento y su inverso es también un movimiento, y ésto lo tendríamos observando que las matrices

son inversas una de la otra, y, por último, la composición (producto) de movimientos es otro movimiento dado que la composición de movimientos se corresponde con el producto de matrices siguientes:

que será un movimiento al tenerse que

y que M₁.M₂ también es ortogonal puesto que se verificaría:

CONSECUENCIA 3ª:

Un movimiento f se denomina traslación si su ecuación matricial es

o, en forma de sistema:

donde el vector se denomina vector de la traslación, y el movimiento f se acostumbra a denotar por .

Pues bien, lo más importante de las traslaciones son los siguientes hechos:

a) Las traslaciones forman un subgrupo normal de Mov(Rⁿ).

b) Las traslaciones distintas de la identidad no tienen puntos dobles.

El hecho a) es consecuencia de que el producto de matrics de la forma

da por resultado una matriz de la forma:

El hecho b) es consecuencia trivial, pues si (a₁,...,a_n) es no nulo, entonces el sistema anterior sería incompatible, haciendose necesario que x_i' = x_i para obtener los puntos dobles.

CONSECUENCIA 4ª:

La notación matricial de que hemos dotado a los movimientos nos permite, para pequeños valores de la dimensión, describir todos los tipos de movimiento del espacio considerado, según sus ecuaciones canónicas.

Consideremos los casos:

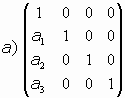
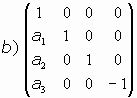
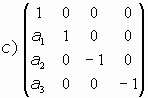
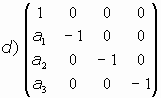
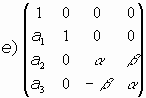
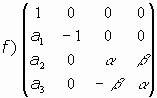
En los casos e) y f) es y , así, podemos considerar siendo .

Estudiemos los casos por los sistemas que producen:

- Caso a):

El sistema en este caso es

sistema ya visto, pues es la traslación de vector o bien la identidad, si a₁=a₂=a₃=0.

- Caso b):

El sistema sería

El sistema de puntos dobles es {0=a₁; 0=a₂; x₃=1/2.a₃}, que es incompatible, salvo que (a₁, a₂)= (0,0).

Tenemos, pues, dos subcasos a considerar:

b₁): (a₁, a₂) = (0, 0)

El conjunto de puntos dobles de f es el plano .

Si calculamos para P(x₁, x₂, x₃) su imágen , se tiene el vector , que es un vector normal al plano p, siempre que , y el vector nulo sí.

Se tiene, pues, que para todo punto P, su imágen es el punto f(P), único, tal que y el punto medio de P y f(P) esté en p.

A un movimiento así se le denomina SIMETRÍA RESPECTO DEL PLANO p.

b₂):

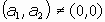
En este caso podemos descomponer el movimiento en dos, de la siguiente forma:

así, pues, f sería el producto (se puede probar que es conmutativo) de la simetría del subcaso anterior y la traslación de vector , que es paralelo al plano p anterior.

Este movimiento se denomina SIMETRÍA CON DESPLAZAMIENTO PARALELO.

- Caso c):

El sistema sería:

Con lo cual el sistema de puntos dobles queda: {0 = a₁, x₂ = 1/2.a₂, x₃ = 1/2.a₃} que es compatible con el caso a₁ = 0. Otra vez es necesario estudiar dos subcasos:

c₁):

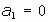
Aqué el conjunto de puntos dobles es una recta de ecuación

Si tomamos un punto cualquiera P(x₁,x₂,x₃), como f(P)=(x₁, a₂-x₂, a₃-x₃), se tiene que es un vector perpendicular a la recta de puntos dobles, y que el punto medio de P y f(P) es que pertenece a la recta de puntos dobles. En definitiva, f verifica que a cada punto P le asocia f(P) de modo que el punto medio pertenece a la recta de puntos dobles y el vector es perpendicular a dicha recta. A este movimiento se denomina SIMETRÍA AXIAL (de eje la recta de puntos dobles)

c₂):

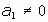
Si descomponemos:

se tiene que f es producto (conmutativo) de la simetría axial anterior y la traslación de vector , que es paralelo al eje de simetría anterior. Tal tipo de movimiento se denomina SIMETRÍA AXIAL CON DESPLAZAMIENTO PARALELO.

- Caso d):

El sistema será:

Solo tendría un único punto doble .

A un punto cualquiera P(x₁, x₂, x₃) le asocia f(P)=(a₁-x₁, a₂-x₂, a₃-x₃), el punto doble PD es es único que es el punto medio entre P y su imágen f(P).

A tal movimiento f se le denomina SIMETRÍA CENTRAL de centro AD.

- Caso e):

Aquí el sistema sería:

Como , luego , el estudio del sistema de puntos dobles nos llevaría a:

como se tiene que

puesto que , tenemos que el sistema es compatible solo en el caso . Tenemos así dos nuevos subcasos:

e₁):

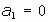
En este caso el conjunto de puntos dobles es la recta de ecuación

cuyo vector director es paralelo a (1,0,0).

Si P=(x₁,x₂,x₃), f(P)=(x₁, a₂+ax₂+bx₃, a₃+ bx₂+ax₃). Su imágen es, pues, un punto con la misma primera coordenada y a la vista de cómo se transforman las dos últimas coordenadas se deduce que f actúa sobre P como un giro de angulo f, en un plano perpendicular a la recta de puntos dobles que `pasa, dicho plano, por el punto P.

A f se le denomina GIRO de eje la recta de puntos dobles.

e₂):

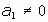
Nuevamente descomponemos:

y siendo el producto conmutativo, f es un producto del giro del caso anterior con una traslación de vector que es paralelo al eje de giro.

Tal movimiento f se denomina GIRO CON DESPLAZAMIENTO PARALELO, o más habitualmente, MOVIMIENTO HELICOIDAL

- Caso f):

Aquí el sistema sería:

Con .

El sistema de puntos dobles es:

Como es

se tiene que existirá un único punto doble PD, cuyas coordenadas no explicitamos, pues solo nos interesa su existencia.

Además, como

que conmutan, y se tiene que f es el producto de un giro por una simetría planar, de plano perpendicular al eje de giro. Tal movimiento se denomina SIMETRÍA CON ROTACIÓN.

COMENTARIOS FINALES DE LA CONSECUENCIA 4ª:

1) Según los puntos dobles de los movimientos en R³ tendríamos los siguientes casos:

Con ningún punto doble:	TRASLACIONES, GIRO HELICOIDAL, SIMETRÍA CON TRASLACIÓN
Con un único punto doble:	SIMETRÍA CENTRAL, SIMETRÍA CON ROTACIÓN
Con una recta de puntos dobles:	GIRO, SIMETRÍA AXIAL
Con un plano de puntos dobles:	SIMETRÍA PLANAR
Todo punto es doble:	LA IDENTIDAD

2) Las traslaciones no son más que el producto de dos simetrías planares de planos paralelos, cuya distancia entre ellos es la mitad del módulo del vector de traslación.

Los giros son también el producto de dos simetrías planares, con planos secantes en el eje de rotación y ángulo entre ambos planos mitad del ángulo de la rotación.

Si trasladamos una simetría planar quedaría dicho movimiento descompuesto, a lo más, en el producto de tres simetrías planares.

Si giramos una simetría planar, otra vez dicho movimiento quedaría, a lo más, como el producto de tres simetrías planares.

Por último, si trasladamos un giro, o viciversa, si giramos una traslación, quedaría a lo más como el producto de cuatro simetrías planares. Y así sucesivamente, etc. etc.

Es justamente este número final, cuatro, el máximo del número mínimo en que podemos descomponer los movimientos del espacio R³ en simetrías planares, y es, en definitiva, la tesis del Teorema de Cartan-Dieudonné, que a continuación enunciamos y trataremos de probar para el caso X = Rⁿ, con lo cual hablaremos ya de simetrías hiperplanares.

EL TEOREMA DE CARTAN-DIEUDONNÉ:

Sea X un espacio Afín Euclideo, con . Entonces todo movimiento se puede escribir como la composición (producto) de, a lo más, n+1 simetrías hiperplanares.

Para la demostración, podemos suponer que f no es la identidad en X, puesto que en dicho caso, f=Id_X, tomando cualquier hiperplano H, consideremos que es s_H la simetría hiperplanar respecto de dicho hiperplano, se tiene que

f=Id_X=s_H^o s_H=s_H²

por lo cual, la identidad se descompondrá en dos simetrías hiperplanares.

Luego, si f no es la identidad en X, debe existir un punto P₀ de X que no sea doble, es decir, con f(P₀) distinto de P₀.

Pot tanto, podemos considerar el punto medio del segmento de extremos P₀ y f(P₀), que denominaremos M₀, y que es

(entenderemos la suma de vectores con "puntos", estos últimos considerados como vectores de posición de dichos puntos, así, , con O orígen de coordenadas.

A partir de M_o y del vector , podemos construir el hiperplano definido por dicho punto y con vector "normal" el dado, es decir, podemos crear el hiperplano .

Obviamente, se puede probar que dicho hiperplano lo podemos expresar de la forma:

Además, si R es un punto doble de f, , entonces, por ser f un movimiento se tiene que

con lo cual se tiene que

y s_H la simetría hiperplanar verifica evidentemente que y viciversa.

Consideremos ahora el movimiento , producto de la simetría hiperplanar s_H con nuestro movimiento de estudio f. Tendríamos:

a)

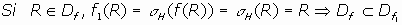
b) , por hipótesis, sin embargo, , con lo cual .

Por tanto, deducimos que:

[*]

Como , por hipótesis, se tendrían los siguientes casos:

1º. Si , entonces D_f es un hiperplano, luego f es una simetría hiperplanar, es decir, f=s_Df.

2º. Si , entonces consideramos , con lo cual, por [*] se tendrá que .

Pero si , pero esto es una contradicción, puesto que es .

Luego, .

Es decir,f es el producto de dos simetrías hiperplanares.

3º. Si , entonces con , con lo cual f₁ es la composición de a lo más 2 simetrías hiperplanares, así, f es a los más la composición de tres simetrías hiperplanares.

4º. Si llegamos por analogía a la conclusión de que f es a lo más la composición de cuatro simetrías hiperplanares.

... ... ... ...

... ... ... ...

nº. Si , deduciremos también que f₁ es a lo más la composición de n-1 simetrías hiperplanares, y f de a lo más n simetrías hiperplanares.

Por último, en el caso , se tiene al final que f es la composición de a lo más n+1 simetrías hiperplanares.

Con esto termina la prueba del teorema.

UN EJEMPLO TEÓRICO:

Sea la traslación de vector .

Queremos aplicar el proceso del Teorema de Cartan-Dieudonné al movimiento .

Como en este caso ningún punto es doble por ser una traslación, sea P un punto cualquiera de X, y consideremos el hiperplano

Consideremos .

Como . Calculemos D_f1.

a) . Así,

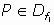
b) Sea .

Para justificar el último paso de esta igualdad tengamos en cuenta que:

1. (puesto que )

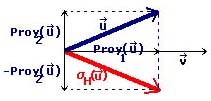
2. Y si observamos gráficamente la siguiente figura

se tiene:

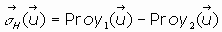
Así, pues, se tiene que , luego como es doble , entonces para todo punto de H' es doble, así una variedad afín que contenga a un hiperplano, o es un hiperplano o es todo el espacio. Pero si (contradicción).

Luego es , así , luego Y ya tendríamos descompuesta la traslación en producto de dos simetrías hiperplanares.