Max Zorn fue un matemático alemán, nacido en el año 1906 en la población de Krefeld, a unos 20 kms de Dusseldorf, realizando sus estudios de matemática en la Universidad de Hamburgo, con Emil Artin. Se doctora en esta Universidad en el año 1930 con una tesis sobre Algebras Conmutativas, y consigue en esa misma época excelentes logros por los cuales la Universidad de Hamburgo le concede al poco tiempo un Premio Extraordinario.

Sin embargo, aunque Zorn no era judío, el nazismo que ya tenia gran fuerza en Alemania le obliga a exilarse a los Estados Unidos en el año 1934, trabajando en la Universidad de Yale entre los años 1934 y 1936, hasta trasladarse a la Universidad de California donde permanecería hasta 1946.

Fue durante el periodo de Yale cuando enunció una proposición que llamó “Principio del Máximo” en un artículo que publicó en el año 1935 en el Boulletin de la American Mathematical Society y que, sin embargo, la posterioridad lo conoce por el nombre que le dio el matemático John Tukey, uno de sus contemporáneos: “El Lema de Zorn”.

Trabajó a partir de 1946, y hasta su jubilación en el año 1971, en la Universidad de Indiana, incursionando en diversos temas tales como los Espacios de Banach y cuestiones diversas de Topología General y Álgebras Conmutativas, así como problemas concretos tales como el estudio de la Hipótesis de Riemann. En realidad, aunque siempre le acompañó la fama creada por el enunciado de su Lema, nunca dejó de estudiar problemas de la actualidad matemática de su tiempo, hasta su muerte en el año 1993, acaecida en Bloomington, Indiana (EEUU).

Imagen que figura en la Web de la Universidad St. Andrews, Escocia
http://www-groups.dcs.st-andrews.ac.uk/~history/Mathematicians/Zorn.html

1. Una breve introducción:

Para exponer claramente el enunciado de Zorn es necesario que repasemos, al menos de manera breve, algunos conceptos básicos de orden en conjuntos generales.

Relación de orden
Una relación definida sobre los elementos de un conjunto de forma que sea reflexiva, antisimétrica y transitiva es una relación de orden. Tal relación permite comparar dos elementos dados y nos permite indicar cuál de ambos está “antes” en dicho orden y cuál es el que está “después”.

Si en el conjunto hay pares de elementos que no son comparables, esto es, de los cuales no se puede decir cuál está “antes” y cuál está “después”, la relación se dice que es de orden parcial, y, si por el contrario todos los pares de elementos del conjunto son comparables, la relación se denomina de orden total.

En definitiva, un conjunto dotado de una relación de orden es un conjunto ordenado. El orden puede ser total o no según que dos cualesquiera elementos del conjunto sean comparables con dicho orden, o que, sin embargo, existan parejas de elementos que no se puedan comparar con él. Un orden parcial indica, pues, que existen pares de elementos de los que no se pueda decir cuál de los dos está “antes” que el otro en dicho orden.

Tanto si en el conjunto que se considere existe un orden total, o bien un orden parcial, siempre pueden seleccionarse elementos del mismo conjunto sobre los cuales el orden del conjunto global sea un orden total. El conjunto de estos elementos seleccionados es lo que llamamos una cadena. Una cadena C, pues, es un subconjunto de un conjunto A al menos parcialmente ordenado y tal que los elementos de C están totalmente ordenados.

Un conjunto se dice bien ordenado, o, simplemente, dotado de un buen orden, si toda parte no vacía del mismo admite un primer elemento. Es inmediato que si un conjunto está bien ordenado, también está totalmente ordenado, pues bastará tomar una parte de solo dos elementos y uno de ellos, por el buen orden existente, será el primero, es decir, el que está “antes” en dicho orden.

Cotas
Un conjunto A dotado al menos de un orden parcial del tipo “menor o igual que” se dice superiormente acotado, o mayorado, por un elemento p si ningún elemento x del conjunto A es mayor que el elemento p. Si todos los elementos de A fueran comparables con p esto sería equivalente a decir que todo elemento de A “es menor o igual que” el elemento p. El elemento p se dice cota superior de A, o mayorante de A.

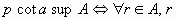no(>p)

Análogamente se define el concepto de inferiormente acotado, o minorado. Los elementos que no son mayores que ningún elemento de A se llaman cotas inferiores de A, o minorantes de A.

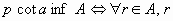no(< p)

Elementos maximales y minimales
Un elemento maximal de un conjunto A al menos parcialmente acotado es un elemento de A tal que ningún otro elemento de A es mayor que él. Es, dicho de otro modo, un elemento del conjunto A que es cota superior del mismo.

Un elemento minimal de un conjunto A al menos parcialmente acotado es un elemento de A tal que ningún otro elemento de A es menor que él. Es, dicho de otro modo, un elemento del conjunto A que es cota inferior del mismo.

Si el conjunto A estuviera totalmente ordenado, entonces, un elemento maximal, si existe, se denomina máximo, y es único. Lo mismo ocurre con un elemento minimal, al cual denominaremos mínimo de A y es, también, único.

En definitiva, podemos escribir las relaciones simbólicas siguientes:

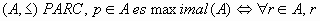no(>p>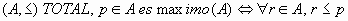

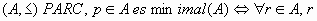no(< p)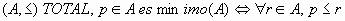

Si el conjunto de las cotas superiores de A estuviera totalmente ordenado, su elemento mínimal, caso de existir, sería único y elemento mínimo de dicho conjunto de cotas superiores, el cual se dice que es el supremo del conjunto A, el cual, si perteneciera al conjunto A, sería también el máximo de A.

Por analogía, si el conjunto de las cotas inferiores de A estuviera totalmente ordenado, su elemento maximal, caso de existir, sería único y elemento máximo de dicho conjunto de cotas inferiores, el cual se dice que es el ínfimo del conjunto A, el cual, si perteneciera al conjunto A, sería también el mínimo de A.

Si el orden del conjunto A que contiene a la cadena C es un orden total, entonces tanto el supremo como el ínfimo de C, caso de existir, son elementos únicos, es decir existe un solo elemento maximal que llamaremos máximo y un solo elemento minimal que llamaremos mínimo.

En realidad, un conjunto en el que cualquier cadena esta mayorada, o sea, que admite cota superior, es un conjunto de tipo inductivo, esto es, ordenado inductivamente. Si, además, admite una cota superior o mayorante mínimo (o supremo), diremos que el conjunto es fuertemente inductivo.

2. El enunciado de Zorn:

Nos hacemos ahora una pregunta fundamental ¿cuándo un conjunto total o parcialmente ordenado admite elementos maximales?. ¿Tiene algo que ver con que el conjunto sea inductivo? ¿tiene algo que ver con que Esta es la proposición:

Si en un conjunto, A, parcialmente ordenado, toda cadena está mayorada, esto es, si se trata A de un conjunto inductivo, entonces A admite al menos un elemento maximal.

Ya el mismo Zorn explicitó cómo su enunciado o “Principio del máximo” como originalmente le llamaría, resultaba ser equivalente a algunos enunciados clave de la matemática, como el Axioma de Elección o el Axioma de Zermelo de la buena ordenación, sin embargo, hoy dia conocemos decenas de proposiciones que son equivalentes a este Lema.

3. Proposiciones equivalentes al Lema de Zorn:

Detallamos los enunciados de algunos resultados famosos en la Matemática de los que se puede probar su equivalencia con el Lema de Zorn:

El Axioma de Haussdorff:
Para todo conjunto A parcialmente ordenado existe al menos una cadena maximal.

El Axioma de Zermelo:
Todo conjunto A puede ser dotado de un buen orden, es decir, puede ser bien ordenado.

El Axioma de Elección:
Para todo conjunto A puede definirse una función de elección, es decir, una aplicación f del conjunto potencia p(A) exceptuando el vacío, en el conjunto A, que hace corresponder a toda parte no vacía E de A un elemento f(E) de E, que se denomina “elemento distinguido de E por la función de elección”, o bien, “elemento elegido de E”.

El Principio Minimal:
Dado un conjunto A ordenado parcialmente por la relación de inclusión, si para cada una de las cadenas que se puedan formar hay al menos un elemento contenido en todas las cadenas, entonces el conjunto A tiene al menos un elemento minimal.

Lema de Tukey:
Toda familia no vacía de carácter finito tiene un elemento maximal.
(una familia F de conjuntos es de carácter finito si y solo si para toda parte finita de un elemento F es también elemento de F, y además, todo conjunto S tal que todas sus partes finitas son elementos de F también pertenece a F)

Lema de Kuratowsky:
Toda cadena en un conjunto ordenado está contenida en una cadena maximal.

Teorema de Tijonov:
El producto cartesiano de una colección de espacios topológicos compactos es compacto respecto a la topología producto.

4. Una demostración de equivalencia:

Entre las muchas proposiciones que equivalen el Lema de Zorn y de las cuales hemos citado algunas en el anterior apartado de esta exposición, podemos elegir el caso del Axioma de Haussdorff y probar de una forma sencilla la equivalencia entre las dos proposiciones. La demostración obviamente consiste en probar que el Lema de Zorn implica al Axioma de Haussdorff, y, recíprocamente, que el Axioma de Aussdorff implica el Lema de Zorn.

- Demostración de que el Lema de Zorn implica el Axioma de Haussdorff:

Se trata de probar que en todo conjunto A al menos parcialmente ordenado, existe una cadena maximal, esto es, que el conjunto de todas las cadenas del conjunto A tiene elementos maximales. Para probarlo construiremos el conjunto K de dichas cadenas y veremos que se trata de un conjunto inductivo, por lo que al aplicarle el Lema de Zorn resultará que posee elementos maximales, que es lo que pretendemos probar y lo que, en resumen, afirma el Axioma de Haussdorff.

Por tanto:

Sea 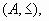parcialmente ordenado.

Sea C_i una cadena del conjunto A, esto es, un subconjunto totalmente ordenado de A:

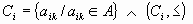Totalmente ordenado

Y sea 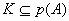el conjunto de todas las cadenas C_i que se puedan formar en tal conjunto A:

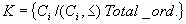
Vamos a probar que 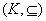es inductivo, esto es, existen elementos mayorantes de cualesquiera cadenas. Para ello construyamos dentro de K una cadena C_c, esto es, una cadena de cadenas de elementos de A: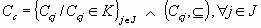

Totalmente ordenado

y construyamos finalmente el conjunto unión de todas las cadenas, del cual veremos que es también una cadena de 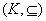y además es elemento mayorante del mismo. En efecto:

Es una cadena, pues



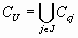
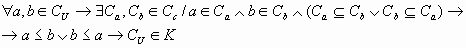
Veamos que K, conjunto de todas las cadenas, es inductivo, pues la misma cadena C_U resulta ser un elemento mayorante de K:

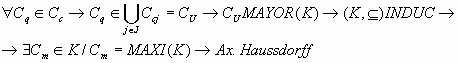
- Demostración de que el Axioma de Haussdorff implica el Lema de Zorn:

Se trata ahora de probar que si en conjunto A, al menos parcialmente ordenado, hay cadenas maximales, entonces, caso de que el conjunto A sea inductivo, tiene también elementos maximales, que es la afirmación del Lema de Zorn.

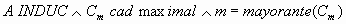
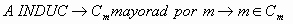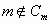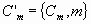Sea pues si entonces la cadena sería maximal y no lo sería 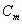, por tanto, ha de ser m elemento maximal de .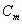

Además, también m es maximal de A, pues de existir otro m’ >m entonces la cadena 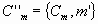sería maximal, y no lo sería 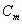. Por tanto, existe un elemento maximal m del conjunto inductivo A (Lema de Zorn)

5. Referencias:

DUBREIL, P., DUBREIL-JACOTIN, M.l., Lecciones de Algebra Moderna. Ed. Reverté, 1971.
HALMOS, Paul R., Teoría Intuitiva de Conjuntos, CECSA, México, 1965.
QUEYSANNE, Michel , Álgebra básica, ED. VICENS-VIVES, Barcelona, 1971.

Carlos SÁNCHEZ CHINEA
casanchi@teleline.es
28 febrero 2004

---

Más artículos de Matemática

---