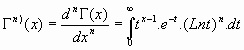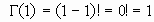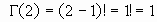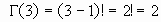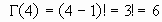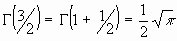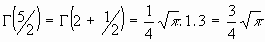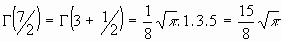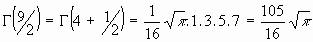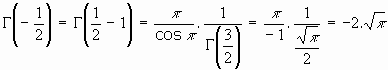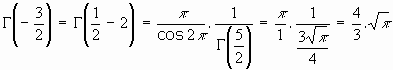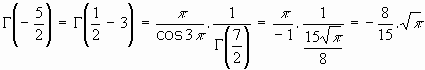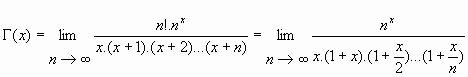
02. La representación
integral:
Es fácil probar la equivalencia entre la expresión del limite y la expresión integral. Veamos a continuación, como
ejemplo, la demostración de la equivalencia para Re(x)>0 con la integral de Euler.
03. Un teorema de equivalencia:
Obtengamos, desde la integral de Euler, la expresión de la función gamma como el límite del cociente antes
indicado.
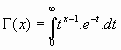
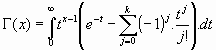
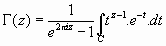
En efecto:
De ser 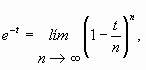 se tiene
se tiene
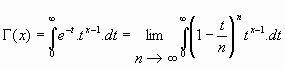
Haciendo el cambio de variables 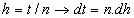 ,
se tiene:
,
se tiene:
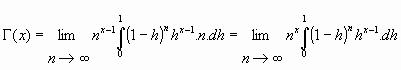
[1]
Aplicando la fórmula de resolución por partes (
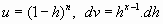 ):
):
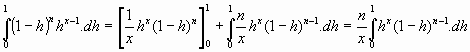
Repitiendo del proceso con la nueva integral, se tiene:
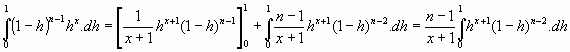
y continuando el procedimiento, van apareciendo los términos que buscamos, que sustituidos en [1]:
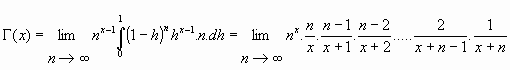
Con lo cual:
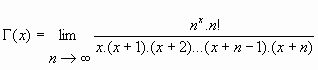
Las propiedades básicas de la función gamma podemos razonarlas, en definitiva, tanto desde la expresión integral
como desde la expresión infinitesimal en la forma de límite de un cociente.
04. Las propiedades básicas:
1.La ecuación funcional:
Si resolvemos por partes la integral de Euler, se tiene:
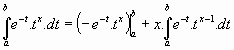
y, para los límites 0 e µ :
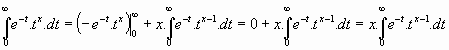
O sea:
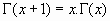
que se puede generalizar de la forma:
|
|
Para x = 1, es
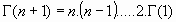
Y siendo
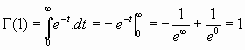
Se tiene, que, para cualquier número natural n > 0, es:
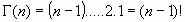
2.La identidad de Weierstrass:
Se tiene que
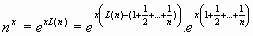
Y llamando
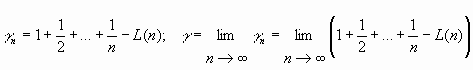
(constante de Euler)
podemos escribir:
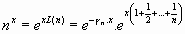
entonces:
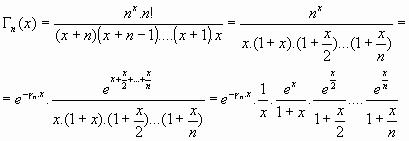
pasando al límite:
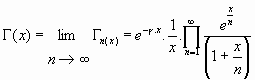
o bien:
|
|
(Identidad de Weierstrass)
3.La fórmula del complemento o la reflexión:
Desde la Identidad de Weierstrass podemos escribir:
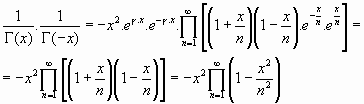
y siendo, por la ecuación funcional de Euler:
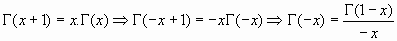
se tiene, al sustituir:
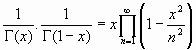
y como es
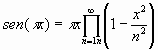 , se obtiene finalmente:
, se obtiene finalmente:
|
|
(Fórmula del complemento o la reflexión, de Euler)
Esta fórmula nos permite calcular rápidamente diversos valores de la función, por ejemplo:
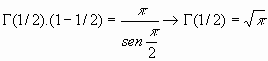
4.Logaritmo:
Tomando logaritmos neperianos en la fórmula de Weierstrass, se tiene:
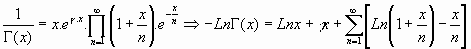
o bien:
|
|
5.Derivada:
Podemos obtener la derivada desde la expresión integral de Euler, o bien haciendo la derivada logarítmica en la expresión del logaritmo anterior.
Desde la integral:
Derivando la expresión integral, se tiene:
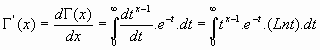
y las derivadas sucesivas:
|
|
La derivación logarítmica:
En cuanto a la derivada logarítmica:
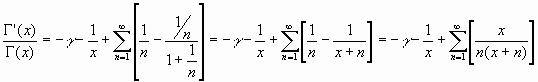
quedando, finalmente, para la expresión de la derivada:
|
|
6.Una relación con la Función Beta de Euler:
La llamada Función Beta de Euler, es una expresión integral de la forma
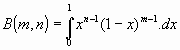
[2]
y tiene, entre otras particularidades, la de estar relacionada con la función gamma de una forma que resulta extremadamente útil a la hora de demostrar algunas de sus propiedades básicas. Admite diversas expresiones, como por ejemplo:
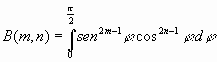
[3]
que se obtiene de [2] sin mas que hacer el cambio de variables
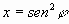 .
.
Veamos la demostración de la relación
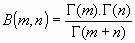
En efecto:
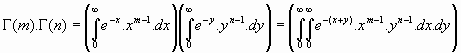
haciendo los cambios
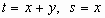 , se tiene:
, se tiene:
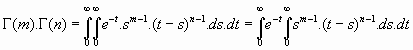
Hacemos ahora el cambio
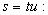
Se tiene:
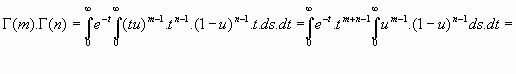
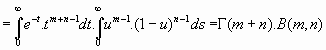
y, en definitiva:
|
|
7.La deducción de la Fórmula Duplicativa de Legendre:
Usando la expresión [3] para la función beta, se tiene que:
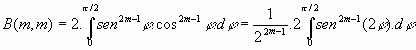
y con el cambio de variables
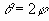 :
:
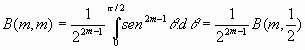
y, a partir de la relación con la función gamma, del apartado anterior:
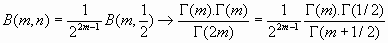
por tanto:
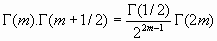
o bien:
|
|
8.Generalizando la Fórmula de Legendre. La Fórmula multiplicativa de Gauss:
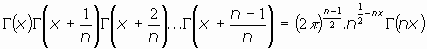
Esta expresión, que puede probarse por inducción, generaliza la anterior forma duplicativa de Legendre.
05. Algunos valores:
Podemos obtener valores puntuales desde las expresiones deducidas anteriormente, que nos pueden dar una
idea de cómo varía la función gamma en el campo real.
1.Desde la ecuación funcional:
Para n entero positivo:
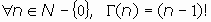
ejemplos:
2.Desde la fórmula del complemento:
... ... ... ...
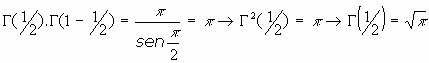
3.Desde la fórmula de Legendre:
Para n entero positivo:
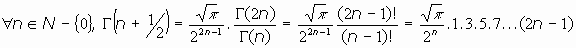
Ejemplos:
... ... ... ...
4.Combinando la fórmula del complemento con la de Legendre:
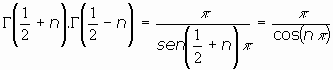
o bien:
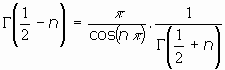
Ejemplos:
... ... ... ...
06. Una representación gráfica:
Gráficamente, en la representación de la función gamma se observan los saltos de discontinuidad infinitos
para los enteros negativos:
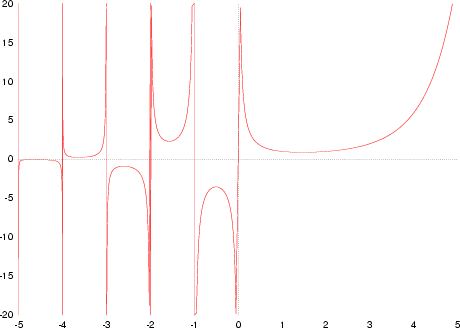
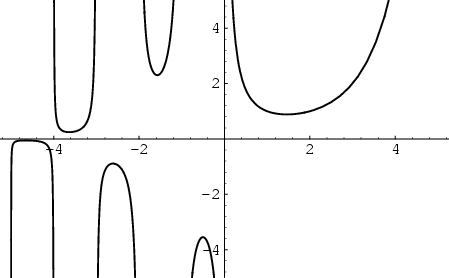
Acercando más la imagen:
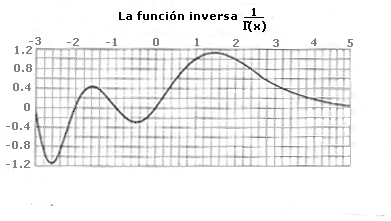
También se observa la continuidad de la función inversa:
07. Referencias:
Abramowitz, M. and Stegun, C. A. (Eds.). Gamma (Factorial) Function and Incomplete Gamma Function. §6.1
and 6.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 255-258 and 260-263, 1972.
Arfken, G. The Gamma Function (Factorial Function). Ch. 10 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 339-341 and 539-572, 1985.
Artin, E. The Gamma Function. New York: Holt, Rinehart, and Winston, 1964.
Borwein, J. M. and Zucker, I. J. Elliptic Integral Evaluation of the Gamma Function at Rational Values of Small
Denominator. IMA J. Numerical Analysis 12, 519-526, 1992.
Davis, P. J. Leonhard Euler's Integral: A Historical Profile of the Gamma Function' Amer. Math. Monthly 66,
849-869, 1959.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.
Magnus, W. and Oberhettinger, F. Formulas and Theorems for the Special Functions of Mathematical Physics.
New York: Chelsea, 1949.
Spanier, J. and Oldham, K. B. The Gamma Function and The Incomplete Gamma and Related Functions. Chs. 43
and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge
University Press, 1990.