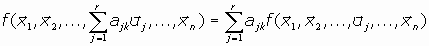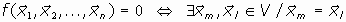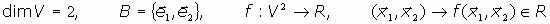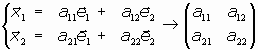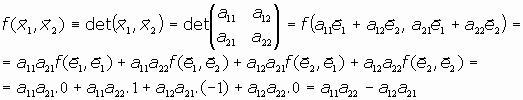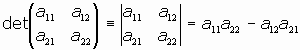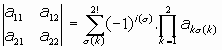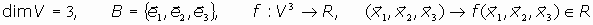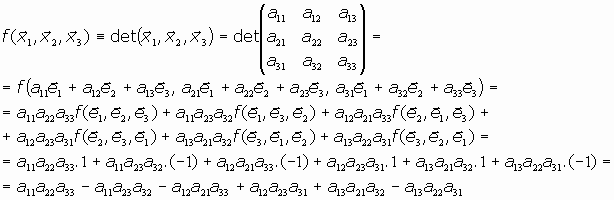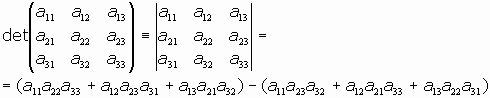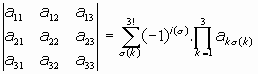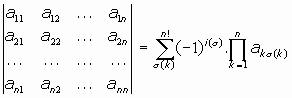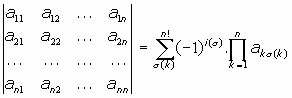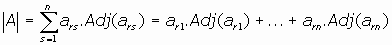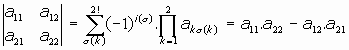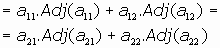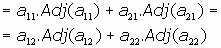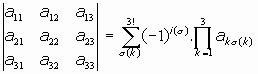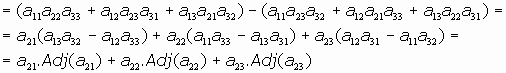Más artículos de Matemática
A propósito del Determinante
En la actual Educación Matemática el concepto de Determinante parece estar, desde su presentación a los estudiantes del nivel secundario, indefectiblemente unido al concepto de Matriz Cuadrada.
Sin embargo, el concepto de Matriz fué usado por primera vez en el año 1850 por James Joseph Sylvester (1814-1897), siendo desarrollado (operaciones, matriz inversa, etc.) por Sir Arthur Cayley (1820-1895) a partir de 1858 en su "Memoria sobre la teoría de matrices", mientras que la idea de determinante había sido inventada por Leibniz (1646-1716) en 1693, incluso hay que decir que, independientemente, los determinantes eran ya usados por el japonés Takakasu Seki Kowa (1642-1708). Debemos a Sir Thomas Muir (1844-1934) una descripción global de la teoría de determinantes, desde su descubrimiento por Leinitz hasta el año 1920.
Gottfried Wilhelm Von Leibniz
Takakasu Seki Kowa
James Joseph Sylvester
Sir Arthur CayleyEl hecho de que el concepto de determinante se presente en la actualidad con una definición altamente elaborada y la no siempre muy clara necesidad de su utilización en la resolución de los problemas fundamentales de la Matemática de nuestro tiempo ha hecho que se levanten voces contrarias a su inclusión en la construcción del Algebra Lineal, de lo cual es una muestra el artículo del Prof. Sheldon Axler de 1995 titulado "¡Abajo los determinantes!". (Sheldon Axler es en la actualidad profesor del College of Science and Engineering, de la Universidad del Estado de San Francisco, USA).
Sir Thomas Muir
Sheldon AxlerEn las líneas que siguen mostramos la definición de determinante como una forma multilineal alternada de un espacio Vn en R, con una condición de contorno para la base canónica del espacio V.
UNA DEFINICIÓN:
Llamamos determinante real del espacio n-dimensional V referido a la base canónica
de V, o determinante de orden n, a una forma multilineal alternada de Vn en R, con la condición de hacer corresponder la unidad del cuerpo R a dicha base, esto es:
Detallemos la definición:
La forma:
Dado un espacio vectorial finitodimensional, V, con dimensión n, sobre un cuerpo K, una forma de Vn es una aplicación,f, de Vn en K, que, por ser isomorfo el espacio V a Kn, podemos expresarla así:
Lineal:
Dicha forma será n-lineal si es lineal con respecto a cada uno de sus argumentos, esto es, la variación de uno de sus argumentos implica que la forma f varíe de forma lineal:Si es
para algún k, entonces la función será:
Alternada:
Una forma lineal será alternada si se anula cuando dos al menos de sus argumentos son iguales.
Una consecuencia elemental:
Es inmediato que toda forma alternada es también antisimétrica, es decir, al cambiar de orden dos de los argumentos la forma cambia de signo.Para verlo bastará considerar que dos argumentos sean iguales y suma de dos vectores. Se tiene, prescindiendo por comodidad de los subíndices:
EL DETERMINANTE DE ORDEN 2:
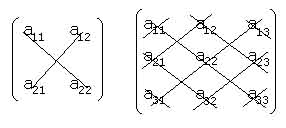
Veamos el caso de que el espacio V sea bidimensional:
Sean las expresiones de ambos vectores en la base B canónica:
(expresión de los vectores en forma tabular)
En definitiva, es:
Es decir, el determinante de orden 2 resulta ser, referido a ambos vectores:
"la suma de los productos de las componentes de ambos vectores afectados por el signo correspondiente a la signatura de la permutación de los segundos subíndices cuando los primeros subíndices se encuentran en permutación principal".
o, si usamos la nomenclatura de tabla:
"resulta ser la suma de los productos de los elementos de la tabla de forma que en cada producto hay un elemento de cada fila y un elemento de cada columna, estando cada producto afectado por el signo correspondiente a la signatura de la permutación de los segundos subíndices cuando los primeros se encuentran en permutación principal"
Podemos escribir la expresión:
EL DETERMINANTE DE ORDEN 3:
Si es tridimensional el espacio V:
Sean las expresiones de ambos vectores en la base B canónica:
(expresión en forma tabular)
(hemos prescindido de los términos que se hacen nulos por tener dos de los vectores básicos iguales)En definitiva, es:
Es decir, el determinante de orden 3 resulta ser, referido a a los tres vectores:
"la suma de los productos de las componentes de los tres vectores afectados por el signo correspondiente a la signatura de la permutación de los segundos subíndices cuando los primeros subíndices se encuentran en permutación principal".
o, si usamos la nomenclatura de tabla:
"resulta ser la suma de los productos de los elementos de la tabla de forma que en cada producto hay un elemento de cada fila y un elemento de cada columna, estando cada producto afectado por el signo correspondiente a la signatura de la permutación de los segundos subíndices cuando los primeros se encuentran en permutación principal"
Podemos escribir la expresión:
GENERALIZANDO AL DETERMINANTE DE CUALQUIER ORDEN n:
(donde es el índice de la permutación de los segundos subíndices, es decir, el número de inversiones que presenta dicha permutación)
Notas aclaratorias:
- Una permutación principal de n digitos enteros, es aquella que sigue el orden natural:123...n.
- Una inversión en una permutacion es un par de digitos que se encuentra dispuesto en orden contrario al orden que tendrían en la permutación principal.
- El índice de una permutación es el número de inversiones, y la signatura de una permutación es (-1) elevado a su índice.
- Por ejemplo, la permutacion 132 tiene una inversion (32) pues los digitos 3 y 2 figuran en un orden contrario al orden natural, por tanto su índice es i=1, y su signatura es (-1)1 =-1
- Otro ejemplo: la permutación 312 tiene dos inversiones, (31) y (32), por lo que su indice es i=2 y su signatura es (-1)2 =1
LA REGLA DE SARRUS:
Es una regla memotécnica que observamos en los determinantes de orden 2 y de orden 3, aunque no así en los de orden superior:
"El determinante de una tabla cuadrada de números es la suma de los productos de las diagonales descendentes de izquierda a derecha menos la suma de los productos de los elementos de las diagonales ascendentes"
MENOR COMPLEMENTARIO. ADJUNTO:
Considerando el determinante de una matriz cuadrada, llamamos Menor complementario del elemento aij de la misma al determinante de la submatriz que se obtiene eliminando en la matriz dada la fila y la columna que se interceptan en dicho elemento aij.
Se define el Adjunto del elemento aij como el producto de (-1)i+j por el menor complementario de dicho elemento:
Adj aij = (-1)i+j.a ij El determinante de un conjunto de vectores dispuestos en forma de matriz cuadrada puede obtenerse multiplicando cada uno de los términos de una linea cualquiera (ya sea fila o columna) por sus correspondientes adjuntos.
En el desarrollo del determinante de orden n hay en total n! Sumandos, cada uno de ellos formado por un producto de n términos, uno de cada fila y uno de cada columna.
Esto quiere decir que un determinado término, ars, está en un total de (n-1)! sumandos del desarrollo de los n! sumandos y en cada uno de ellos figura multiplicando a n-1 factores que son uno de cada fila y uno de cada columna de las restantes filas y columnas (filas distintas de la fila r y columnas distintas de la columna s), estos es, ars figura multiplicando a los (n-1)! sumandos del desarrollo de un determinante en donde se ha suprimido al fila r y la columna s, o sea, el adjunto del elemento ars, y como esto se puede hacer para cualquiera de los elementos de una misma línea, ya sea fila o ya sea columna, resulta que cualquier determinante puede desarrollarse por los elementos de una línea al sacar estos factor común en todo el desarrollo, quedando, en definitiva, una expresión del tipo:
- Desarrollo por la fila r:
- Desarrollo por la columna s:
Por ejemplo, en el caso del determinante de orden 2:
Desarrollo por filas:
Desarrollo por columnas:
Veamos también el desarrollo del determinante de orden 3, por ejemplo, por los adjuntos de la segunda fila:
LAS PROPIEDADES BÁSICAS DEL DETERMINANTE:
1. El determinante de una matriz siempre es igual al determinante de su matriz traspuesta.
2. Si en un determinante se intercambian dos líneas paralelas, el determinante cambia de signo.
3. Si un determinante tiene una línea nula, el determinante es nulo.
4. Si un determinante tiene iguales dos líneas paralelas, de determinante es nulo.
5. Si se multiplica una línea cualquiera de un determinante por un mismo número, todo el determinante queda multiplicado por dicho número.
6. Si dos líneas paralelas son proporcionales, el determinante es nulo.
7. La suma de los productos de los elementos de una línea por los adjuntos de una línea paralela es cero.
8. Si todos los elementos de una cierta línea están constituidos por dos sumandos, el determinante de la matriz puede descomponerse en suma de dos determinantes, de modo que en dicha línea aparezca el primer sumando en el primero de los determinantes y el segundo sumando en el segundo determinante, permaneciendo iguales las restantes líneas en ambos determinantes.
9. Si los elementos de una línea son combinación lineal de líneas paralelas, el determinante es cero.
10. Si a los elementos de una línea se le suman los elementos de otra línea paralela multiplicados por cualquier número, el determinante no varía.
Carlos S. CHINEA
casanchi@teleline.es
06 noviembre 2004
Más artículos de Matemática