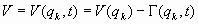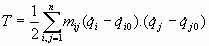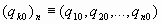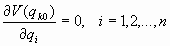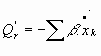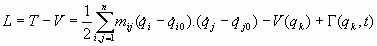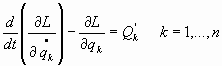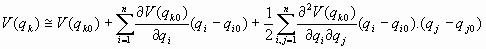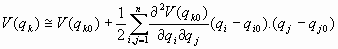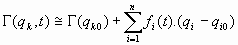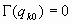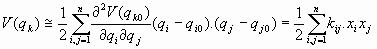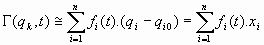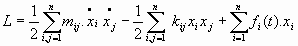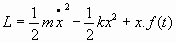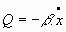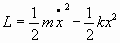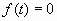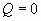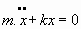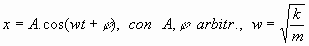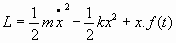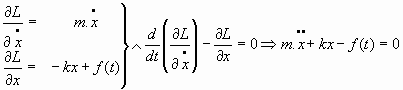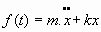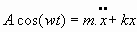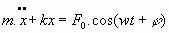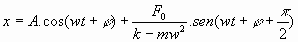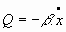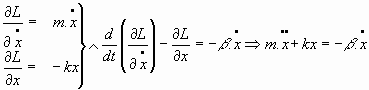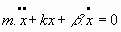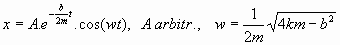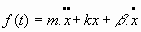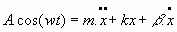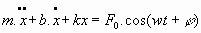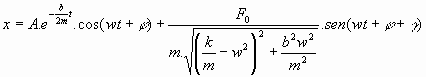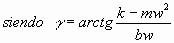1. Introducción. El problema de las oscilaciones:

Existe un especial tipo de movimiento, corriente en los sistemas de partículas, que, por su aplicabilidad a diferentes campos de la física, tanto teórica como experimental, merece una especial atención.

El movimiento oscilatorio corresponde a la situación de un sistema de partículas, S, que está sometido tanto a fuerzas conservativas o como disipativas en el caso más general, con un número cualquiera n de grados de libertad, y de forma que durante un intervalo T de tiempo el mínimo de su energía potencial se encuentra dentro de un entorno, simétrico o asimétrico, repitiéndose periódicamente los valores de tal entorno en el movimiento real del sistema.

El estudio matemático de un sistema oscilante puede hacerse de forma muy precisa construyendo su función de Lagrange, para, a partir de ella, obtener tanto sus ecuaciones de movimiento como las restantes magnitudes cinemáticas y dinámicas.

 

2. Los tipos de sistemas oscilantes:

Si llamamos V a la función potencial de las fuerzas conservativas que actúan sobre el sistema de partículas oscilante, se tiene que V puede depender o no del tiempo.

Llamaremos Oscilador forzado a un sistema oscilante en el que las fuerzas conservativas dependen del tiempo. Siempre es posible descomponer, en este caso, la función potencial en suma de una parte independiente del tiempo y otra parte que si depende del tiempo. A la parte del potencial independiente del tiempo se le puede llamar Potencial de oscilación, y a la parte que sí depende del tiempo Potencial recuperador.

En lo que respecta a las fuerzas no conservativas, es decir, a las fuerzas disipativas que actúan sobre el sistema oscilante, estas podrían o no considerarse nulas durante todo el intervalo de oscilación. El caso en el que las fuerzas disipativas no son idénticamente nulas durante el periodo de oscilación corresponde al oscilador que llamaremos Oscilador amortiguado, o bien, Oscilador con amortiguamiento.

Se define como Oscilador libre a un sistema oscilante que no es forzado ni amortiguado, es decir, un oscilador sobre el que no actúan fuerzas conservativas dependientes del tiempo ni tampoco está sometido a fuerzas de disipación.

Todos los casos, por tanto, ser pueden clasificar así:

- Oscilador no forzado ni amortiguado (Oscilador libre).
- Oscilador no forzado pero con amortiguamiento
- Oscilador forzado sin amortiguamiento.
- Oscilador forzado y amortiguado.

 

3. Los osciladores armónicos:

De lo anterior, por tanto, entendemos que es muy necesario conocer tanto la estructura de la función potencial del campo conservativo en el que se encuentra el sistema oscilante, para poder decidir si se trata o no de un sistema forzado y el grado de su forzamiento, como, también, conocer la función o funciones disipativas para establecer el grado de amortiguamiento del sistema.

Sin embargo, el problema puede ser tratado matemáticamente por aproximación si las funciones indicadoras del potencial de oscilación y del potencial de recuperación son lo suficientemente pequeñas como para poder tomar los primeros términos en una expresión de los mismos mediante un desarrollo de Taylor. El error que se comete en este tipo de aproximación sirve para definir lo que se da en llamar Oscilador armónico

Se define como Oscilador armónico, u Oscilador lineal al sistema oscilante en el que es despreciable (a veces se dice "inferior a una diezmilésima") el error cometido al tomar los dos primeros sumandos no nulos del desarrollo de Taylor de los potenciales de oscilación y recuperación.

Un Oscilador armónico libre es, pues, un oscilador armónico que no está forzado ni amortiguado, esto es, en donde no hay potencial dependiente del tiempo ni fuerzas de disipación.

En los casos de osciladores armónicos amortiguados, con y sin forzamiento, es necesario, para construir sus ecuaciones de movimiento conocer la forma de las funciones de disipación, y, dependiendo de estas funciones, se puede definir un gran número de osciladores armónicos amortiguados, entre los cuales cabe destacar, por su importante aplicación en el contexto de la física experimental, el llamado Oscilador amortiguado de Stokes, cuya condición de definición es la especial forma de las funciones de disipación Q' como suma de los productos de ciertas constantes por las componentes de la velocidad, constantes que se denominan constantes de Stokes.

En lo que respecta, por otra parte, a la forma de las funciones potenciales dependientes del tiempo, en los osciladores forzados, estas pueden tener un comportamiento periódico, generalmente de forma cosinusoidal o sinusoidal, dando lugar a los osciladores denominados Osciladores forzados, con forzamiento periódico.

Se tienen, en definitiva, los casos clásicos siguientes para osciladores armónicos:

- Oscilador armónico libre.
- Oscilador armónico forzado cosenusoidalmente.
- Oscilador armónico forzado sinusoidalmente.
- Oscilador armónico no forzado y con amortiguamiento de Stokes.
- Oscilador armónico forzado cosinusoidalmente y con amortiguamiento de Stokes.
- Oscilador armónico forzado sinusoidalmente y con amortiguamiento de Stokes.

 

4. Tratamiento matemático:

4.1. Tratamiento matemático general:

Veamos en general la construcción de la funciones dinámicas del sistema oscilante, esto es, la función de energía potencial, la función de energía cinética y las funciones de energía disipativa, expresadas en un punto cualquiera del espacio de las fases, es decir, de las coordenadas generalizadas, , y velocidades generalizadas, :

- Energía Potencial:

(Potencial de oscilación: , Potencial recuperador: )
- Energía Cinética:

- Energía Disipativa o amortiguamiento: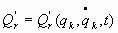

Representaremos por (q_k0)_n al punto del espacio de las fases en donde la energía potencial presenta su mínimo:

cumpliéndose, evidentemente, que

por tratarse de un mínimo.

- Amortiguamiento de Stokes:

- Función de Lagrange o Lagrangiana:

- Ecuaciones de Lagrange:

que son las ecuaciones del movimiento del sistema oscilador.

4.2. Tratamiento matemático de los osciladores armónicos:

Aproximamos la función potencial, tanto de oscilación como de recuperación, mediante los dos primeros términos no nulos del desarrollo de Taylor:

Potencial de oscilación:

y, siendo nulo el término central, por tratarse de la derivada en un mínimo:


Potencial recuperador o de forzamiento:


Y si tomamos el origen de medición del potencial en el punto (q_k0)_n del mínimo, se tendría: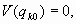


Con lo cual, finalmente, se expresarían ambos potenciales de la manera siguiente:

Potencial de oscilación:

Potencial recuperador:


(llamando, para simplificar, )

Podemos, en definitiva, escribir la lagrangiana de los osciladores armónicos con la expresión:

la cual, al ser sustituida en las ecuaciones de Lagrange, mostrarían las ecuaciones del movimiento del sistema oscilante armónico.

 

5. Ejemplo de obtención de ecuaciones de movimiento en osciladores armónicos unidimensionales:

En el caso de una sola dimensión, se tiene que la lagrangiana se podría expresar por

y el amortiguamiento de Stokes vendría dado por:

 

5.1. Oscilador armónico libre (sin forzamiento y sin amortiguamiento):

Ecuación del movimiento:
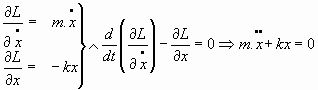
que, al integrarse, da:

 

5.2. Oscilador armónico forzado sin amortiguamiento:

Ecuación del movimiento:

Si el potencial de forzamiento, f(t), es periódico, sinusoidal o cosinusoidal, se puede escribir una expresión del tipo

^, Así, por ejemplo, si se trata del oscilador armónico con forzamiento periódico sinusoidal de ecuación del movimiento dada por
Se tiene, al integrar:

 

5.3. Oscilador armónico no forzado con amortiguamiento de Stokes:

Ecuación del movimiento:
que, al integrar, nos da:

 

5.4. Oscilador armónico forzado y con amortiguamiento:

Ecuación del movimiento:

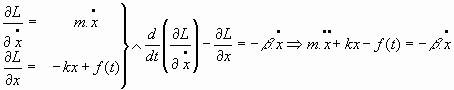
Si el potencial de forzamiento, f(t), es periódico, sinusoidal o cosinusoidal, se puede escribir una expresión del tipo

^,
Para un forzamiento periódico cosinusoidal dado por
Se tiene una solución del tipo

 

---ooo0ooo---

BIBLIOGRAFÍA:

G.W. Bluman and S. Kumei, Symmetries and Differential Equations, Applied Mathematical Science 81, Springer Verlag, New York (1989).

P.E. Hydon, Symmetry Methods for Differential Equations: A Beginner's Guide, Cambridge Texts in Applied Mathematics, Cambridge University Press, New York (2000).

N.H. Ibragimov, Ed., CRC Handbook of Lie Group Analysis of Differential Equations. Volume 1: Symmetries, Exact Solutions, and Conservation Laws, CRC Press, Boca Raton, Florida (1994).

N.H. Ibragimov, Ed., CRC Handbook of Lie Group Analysis of Differential Equations. Volume 2: Applications in Engineering and Physical Sciences, CRC Press, Boca Raton, Florida (1995).

N.H. Ibragimov, Ed., CRC Handbook of Lie Group Analysis of Differential Equations. Volume 3: New Trends in Theoretical Developments and Computational Methods, CRC Press, Boca Raton, Florida (1995).

P.J. Olver, Applications of Lie Groups to Differential Equations, Graduate Texts in Mathematics 107, 2nd edition, Springer Verlag, New York (1993).

H. Stephani, M. MacCallum Ed., Differential Equations: Their Solution using Symmetries, Cambridge University Press, Cambridge, UK (1989).

G. Gaeta, A bibliography on Lie-point symmetries of differential equations and physics, mp_arc 93-119.

---ooo0ooo---

Carlos S. Chinea
casanchi@teleline.es
20 junio 2002

---

Otros artículos de Física

---