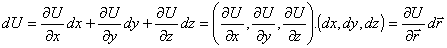Más Artículos de Física
Una Incursión por el Sólido Rígido
Un sólido rígido ideal es un conjunto de partículas mj, cuyas distancias relativas dij=rj-ri, se mantienen constantes. Cuando en los sólidos reales se pueden despreciar los inevitables cambios en la forma y en el volumen, se pueden tratar como sólidos rígidos ideales.Para poder describir la mecánica del sólido rígido es conveniente la elección precisa de los sistemas referenciales necesarios. Esta descripción se simplifica si elegimos tres sistemas de referencia: uno, Kf, fijo en un punto exterior al sólido, otro, k1, fijo en un punto del sólido (x0,y0,z0), con los ejes siempre paralelos a Kf, es decir, no gira con el sólido. Y, finalmente, un tercer sistema referencia, k2, que tendría su origen en el mismo punto origen, (x0,y0,z0), de K1, pero giraría con el sólido.
El movimiento de K2 con respecto a K1 nos permitirá, en definitiva, el estudio de un sólido ideal con un punto fijo, dotado de un movimiento rotacional.
Asimismo, cualquier posición en el espacio del sólido rígido queda determinada con respecto al sistema exterior fijo, Kf, por el vector de posición del origen común de los sistemas K1 y K2, y los tres ángulos (A,B,C) que orientan al sistema K2 con respecto al sistemas K1. En definitiva, el sólido rígido puede estudiarse como un sistema con seis grados de libertad: x0,y0,z0, A,B,C.
1. Las magnitudes fundamentales
1.1. Velocidad
Supongamos que sea w la velocidad instantánea de rotación del sólido y tomemos un
punto P cualquiera para encontrar la expresión de su velocidad.
Si elegimos un punto O del eje de rotación instantáneo del sólido como punto
de referencia, será OP el vector de posición del punto P dado. La velocidad lineal
instantánea de rotación del punto P viene dada por 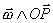 . Por
lo que la velocidad de P será la suma
de la velocidad de traslación del eje de rotación, que es la velocidad de
traslación del sólido, más
su velocidad debida a la rotación. O sea:
. Por
lo que la velocidad de P será la suma
de la velocidad de traslación del eje de rotación, que es la velocidad de
traslación del sólido, más
su velocidad debida a la rotación. O sea:

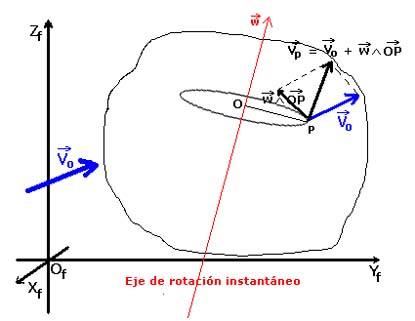
Si en lugar de usar como origen de referencia un punto O del eje de rotación instantáneo, tomamos otro punto O’ cualquiera del sólido, se tiene que su velocidad de este punto O’ respecto al punto O anterior es, de forma análoga:
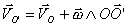
por lo que, si restamos ambas expresiones, se tiene:
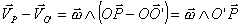
O sea, también se puede expresar la velocidad de P con respecto a otro punto cualquiera O’ por
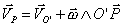
donde ahora es 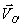 la velocidad
del punto O’ arbitrario de referencia, no
necesariamente la velocidad de traslación del sólido.
la velocidad
del punto O’ arbitrario de referencia, no
necesariamente la velocidad de traslación del sólido.
Se puede enunciar, en definitiva, este teorema:
La velocidad de un punto cualquiera P de un sólido rígido es la suma vectorial de la velocidad de un punto de referencia O cualquiera más la velocidad lineal de P respecto al eje de rotación instantánea del sólido. Si el punto O de referencia elegido es un punto del eje de rotación, la velocidad de este punto O es precisamente la velocidad de traslación del sólido.
Consecuencia: La velocidad instantánea de rotación del sólido es un invariante. Es decir, puede considerarse un vector libre, aun cuando el eje de giro cambia con el origen que se tome. También es un invariante, obviamente, la velocidad V0 de traslación del sólido.
En general los vectores que definen la velocidad de traslación del sólido, Vo, y la velocidad instantánea de rotación, w, son oblicuos, presentando Vo dos componentes con respecto a al eje de giro, una perpendicular y otra paralela.
Muchas veces conviene en utilizar, para simplificar las expresiones, un
punto Cm del
eje de rotación en donde se verifica que la suma total de las expresiones
mj.rj de
la masa de cada
punto por su vector de posición respecto a dicho punto es cero. Este
punto se llama Centro de Masas o
Centro de Inercia del sólido.
1.2. Energía Cinética
Podemos calcular la energía cinética del sólido como la suma algebraica de
las energías cinéticas de
todos los puntos del mismo:
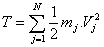
Utilizando la expresión de la velocidad de cada punto con respecto a un origen situado en el eje de rotación del sólido:
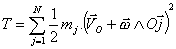
en donde 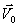 es la velocidad de
traslación del sólido (pues O es
un punto del eje de rotación).
es la velocidad de
traslación del sólido (pues O es
un punto del eje de rotación).
Desarrollando:

Analizamos por separado cada uno de los tres sumandos:
- Primer sumando:
, siendo
la masa total del sólido
Este primer sumando representa la energía cinética debida a la traslación del cuerpo rígido.
- Segundo sumando:
, pues, por una de las propiedades elementales del producto mixto de tres vectores, se verifica que
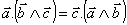
Si elegimos el punto O del eje de rotación de forma que coincida con el Centro de Masas del sólido, se tiene que
por lo que este segundo sumando de la expresión de la energía cinética del sólido lo podemos considerar nulo cuando el punto de referencia es el Centro de Masas.
- Tercer sumando:
pues para dos vectores,
y
, se tiene siempre que es:
Podemos escribir la expresión en notación tensorial, usando las componentes de ambos vectores,
, de la manera siguiente:
donde esla delta de Cronecker.
Si, por simplificar, llamamos
la expresión del último de los sumandos de la energía cinética de rotación del sólido es
.
En definitiva:
La energía cinética total del sólido rígido es una suma de dos términos cuando se referencia al centro de masas del sistema rígido. Un término corresponde a la energía cinética debida al movimiento de traslación del sólido y el otro término es la energía cinética debida a la rotación del mismo.
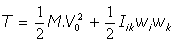
Esta expresión utiliza una notación tensorial para el segundo de los sumandos, apareciendo
el tensor Iik que tiene un importante papel en el estudio dinámico del sólido.
1.3.Lagrangiana y Hamiltoniana
Se expresan de inmediato sin más que restar o sumar, respectivamente, la energía
potencial, U, del sólido. Esta energía potencial depende tanto de la posición del sólido como
de su orientación, es decir, depende de las tres coordenadas del Centro de Masas del sólido
y también de los tres ángulos de Euler que son descritos por un sistema solidario al mismo
con respecto a los ejes del triedro exterior de referencia.
Función de Lagrange:
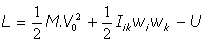
Función de Hamilton:
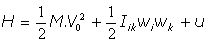
1.4. Momento angular
Supongamos un sólido que tiene un movimiento de rotación en torno a un eje e con
velocidad angular w. Podemos obtener el momento angular de este movimiento de manera muy
sencilla si tomamos como origen del triedro de referencia el Centro de Masas
del sólido. Es decir, el sistema referencial tiene el origen en el Centro de Masas pero no rota con el sólido.
Sea 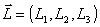 el vector momento angular. Se
tiene, por definición, que es
el vector momento angular. Se
tiene, por definición, que es

Al desarrollar la expresión, se tiene:
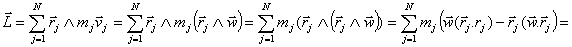
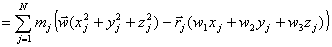
Detallando las tres componentes:
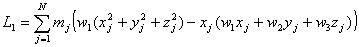
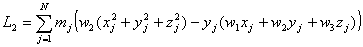
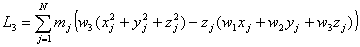
O bien, simplificando:
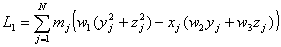

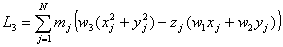
Que podemos escribir en este otro orden:

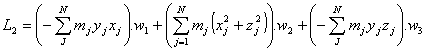
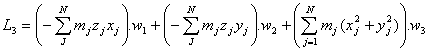
O bien, usando la notación Ijk para los paréntesis:
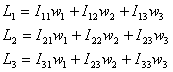
Encontramos, pues, una notación matricial para el Momento Angular:
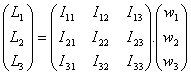
o, más brevemente:
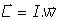
Notemos que este tensor, Ijk, introducido ahora, puede escribirse, cuando llamamos a las coordenadas del punto j de la forma x1j, x2j, x3j, de la forma:

Coincidiendo, en definitiva, con el tensor definido en el apartado 1.2 para expresar la Energía Cinética de
Rotación de Sólido.
1.5. Momento Mecánico
El Momento Mecánico debido a las fuerzas que originan la rotación del cuerpo sólido viene expresado por

Que se puede escribir en función del Momento angular:
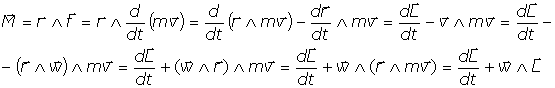
Por tanto, es:

2. Sobre el Tensor de Inercia:
2.1. Expresión de las componentes
Vemos que al expresar las magnitudes fundamentales del movimiento del sólido rígido todas
quedan expresadas en función de un tensor de nueve componentes de la forma

o, en forma continua, de la forma
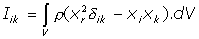
Este tensor, que se denomina Tensor de Inercia del Sòlido, o bien, Tensor de los Momentos de Inercia del Sólido, presenta una estructura simétrica. La forma explícita de sus componentes es
Usando la expresión discreta:
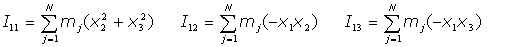
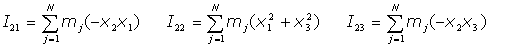
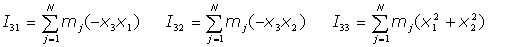
Usando la expresión continua:

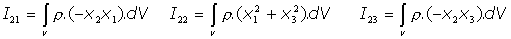
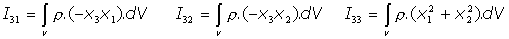
2.2. El tensor de inercia diagonalizado. Ejes y momentos principales
La matriz correspondiente es, pues, una matriz simétrica, y como tal, diagonalizable, esto es, reducible
a la forma diagonal eligiendo convenientemente los ejes de referencia:

En forma diagonal:
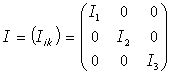
Existen, por tanto, en el movimiento del sólido rígido, unos ejes de referencia con origen en el Centro de Masas y que tienen direcciones tales que el Tensor de Inercia adquiere la forma diagonal. Estos ejes se denominan Ejes Principales de Inercia y las direcciones de los mismos, Direcciones Principales de Inercia. Las componentes no nulas del tensor, que forman la diagonal del mismo, son los Momentos Principales de Inercia, cuyas expresiones son
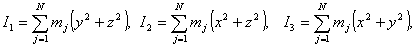
Es decir, los Momentos Principales de Inercia tienen la expresión
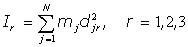
Donde la 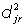 representa el
cuadrado de la distancia de la partícula
de masa mj al Eje Principal xr.
representa el
cuadrado de la distancia de la partícula
de masa mj al Eje Principal xr.
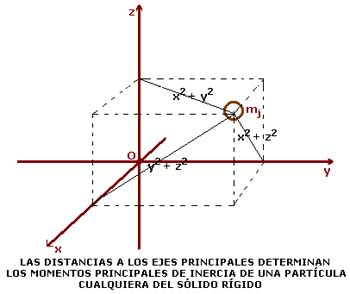
Es inmediato que la suma de dos cualesquiera de los tres momentos principales de inercia es mayor o igual al tercero.
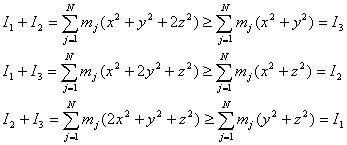
En función de los Ejes Principales de Inercia, las Magnitudes Fundamentales del Movimiento del Sólido Rígido quedan expresadas así:
2.3. Momento de inercia respecto a un eje cualquiera. Teorema de Poinsot- La Energía Cinética:
pues:
- La Energía Cinética de Rotación. Elipsoide de Energía:
De lo anterior, observamos que la energía cinética debida exclusivamente al proceso de rotación es
que permite escribir la ecuación del elipsoide de energía rotacional así:
para la radiación de velocidades
que confieren al solido energia de rotación constante.
- El Momento Angular:
pues:
- El Momento Mecánico:
pues:
- Langrangiana y Hamiltoniana:
Podemos determinar el momento de inercia con respecto a un eje cualquiera en función de los momentos de inercia con respecto a tres ejes de referencia dados. La expresión que se obtiene se conoce en la dinámica del sólido rígido como Teorema de Poinsot.
Así, si consideramos un eje e que forma ángulos 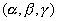 con
respecto a los ejes de referencia, se tendría que el momento de inercia del sólido con respecto al mismo
vendría dado por
con
respecto a los ejes de referencia, se tendría que el momento de inercia del sólido con respecto al mismo
vendría dado por
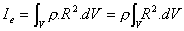
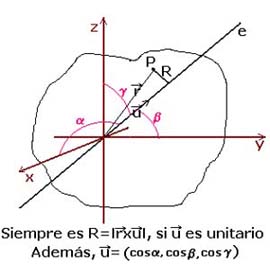
Veamos una expresión de la distancia R de cada punto del sólido al eje e con respecto al cual hemos de calcular el momento de inercia:
 |
Si se trata de un eje que
forma ángulos
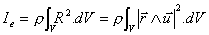
|
Se tiene, entonces:
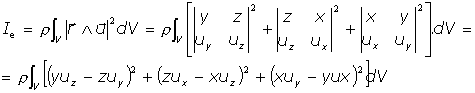
Desarrollando y ordenando resulta:
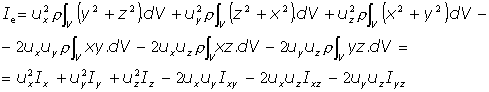
Esta es, en definitiva, la expresión general del Teorema de Poinsot:
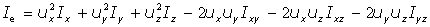
O bien, usando los ángulos de dirección del eje:
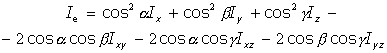
Si los ejes de referencia son los ejes principales de inercia, el tensor estaría diagonalizado, por lo que la expresión del Teorema de Poinsot sería:
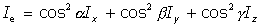
2.4. El Elipsoide de Inercia
Dada la expresión más general del Teorema de Poinsot para un eje de rotación con
dirección dada por los ángulos 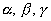 :
:
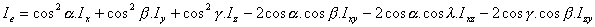
si dividimos por Ie:
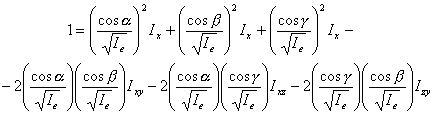
y, haciendo
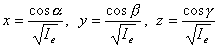
se tiene que

que es la ecuación general de un elipsoide, que se da en denominar Elipsoide de Inercia del Sólido. En el caso de que los ejes de referencia sean los principales de inercia, la expresión de este elipsoide es más sencilla:
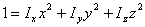
En el Elipsoide de Inercia se puede obtener inmediatamente la distancia al origen
del sistema de referencia de punto P(x,y,z) de corte con el eje de rotación de ángulos
de dirección dados por 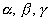 :
:
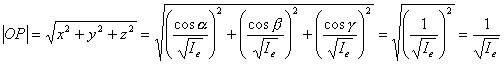
Existe, pues, en todo sólido, un elipsoide
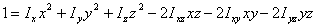
tal que cualquier eje de rotación del mismo con direcciones
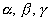 , secciona a éste en
un punto P(x,y,z) cuya distancia al origen de referencia es
, secciona a éste en
un punto P(x,y,z) cuya distancia al origen de referencia es
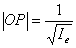
siendo Ie el momento de inercia del sólido con respecto a tal eje de rotación. Y cuyas coordenadas vienen dadas por
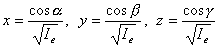
2.5. El Teorema de Steiner
Este teorema nos permite calcular el momento de inercia del solido con respecto a un eje e’, cuando
se conoce el momento de inercia de un eje e, paralelo, que pase por el centro de masas y la distancia
d entre ambos ejes.
Basta elegir un sistema de referencia apropiado, que nos permita hacer coincidir uno de los ejes con un eje coordenado y de forma que el plano que contiene a ambos ejes e y e’ paralelos sea uno de los planos coordenados, tal como se indica en la figura.
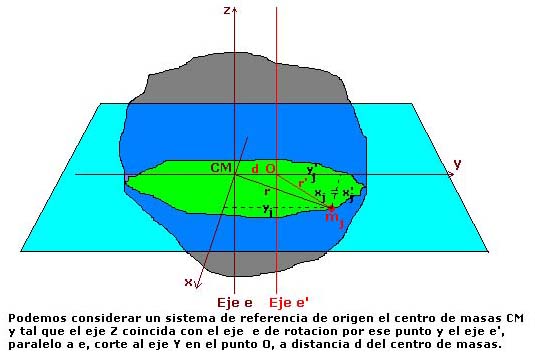
Se tiene:
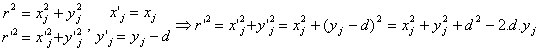
Es decir:
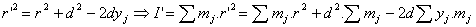
En definitiva
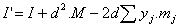
Y como sabemos, por definición del centro de masas, que

resulta nulo el último sumando, por lo que queda

Que es el enunciado del Teorema de Steiner:
El momento de inercia con respecto a un eje paralelo a un eje que pase
por el centro de masas es igual al momento de inercia de este eje mas el producto
de la masa total del sólido por el cuadrado de la distancia entre ambos ejes.
3. Las ecuaciones del movimiento:
Puesto que en la cinemática del sólido rígido figuran 6 grados de libertad (las tres coordenadas
del desplazamiento lineal y los tres ángulos de Euler del movimiento rotacional), son necesarias
seis ecuaciones para la descripción de su movimiento.
Tres de estas ecuaciones se obtienen de analizar la variación de la energía total del sólido en el movimiento traslacional, y las otras tres de la variación de la energía total en el movimiento de rotación.
- Movimiento de traslación:
Si llamamos
a la fuerza total actuante sobre el centro de inercia del sólido, se tiene que la variación de energía en un movimiento infinitesimal
es
y siendo
Al identificar se tiene la ecuación vectorial:
[1]
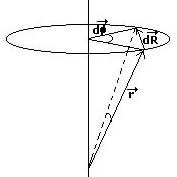
- Movimiento de rotación:
La fuerza
por el desplazamiento rotacional
del centro de inercia del sólido viene expresado de forma sencilla.
Y la diferencial de la energía con respecto a la variable angular:
Podemos expresar el desplazamiento rotacional
con respecto a la variación de los ángulos de Euler:
[1]
con lo cual:

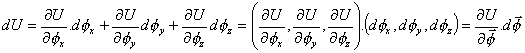
Al identificar obtenemos aquí también la ecuación vectorial correspondiente:
[2]
Expresión escalar de las ecuaciones del movimiento:
De [1]:
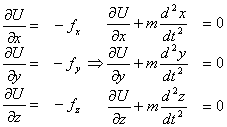
De [2]:
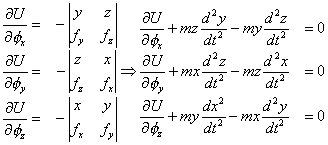
4. Calculando momentos de inercia:
Un sólido cuyos tres momentos principales de inercia son distintos se denomina trompo asimétrico. Si
solo dos de los tres momentos son iguales el sólido se acostumbra a denominar trompo simétrico. Y,
finalmente, si fueran iguales los tres momentos principales de inercia, el sólido se denomina trompo esférico.
Los momentos principales de inercia tienen que ver, fundamentalmente, con la simetría del sólido. Si el sólido admite una cierta simetría se determinan sus ejes principales de forma sencilla puesto que el centro de inercia y las direcciones de estos ejes mantienen la misma simetría.
Si el sólido tiene un plano de simetría, el centro de inercia está en ese plano y dos de los ejes principales se pueden elegir arbitrariamente contenidos en dicho plano de simetría, mientras que el tercer eje es perpendicular a ambos.
Si el sólido tiene un eje de simetría, también el centro de inercia estará en dicho eje de simetría que será también uno de los tres ejes principales de inercia del sólido, mientras que los otros dos ejes serán perpendiculares.
Ejemplo de sólidos con simetría:
- Un sistema de N partículas contenido en un plano.
Veamos en este caso cómo son los momentos principales de inercia.
Sea el plano xy. Esto quiere decir que z = 0, por estar el sistema contenido en un solo plano. Por tanto:
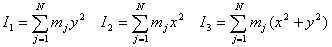
donde las x, y, z representan las componentes de la distancia de cada partícula al centro de masas.
- Un sistema rígido de solo dos partículas:
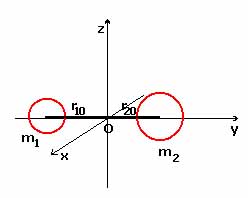
|
En este caso, un eje de simetría atraviesa
a ambas partículas y contiene al centro de inercia O del sistema solido constituido por
ambas, las otras dos coordenadas son nulas, por lo que, si llamamos y al eje que las
contiene, serán x = z = 0, de donde se tiene que es nulo el momento de inercia I2 y son
iguales los otros dos momentos de inercia del sistema: |
Veamos los momentos de inercia:

Ambos momentos de inercia no nulos, I1 e I3, pueden ponerse en función de la distancia d entre las dos partículas:
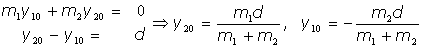
sustituyendo en los momentos de inercia:
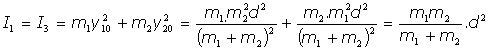
- Momentos principales de inercia de una varilla homogénea de superficie transversal despreciable, con masa M y longitud l.

|
Si llamamos Ix, Iy, Iz a los momentos principales de inercia con respecto a los respectivos ejes x, y, z, deducimos que son iguales los momentos Ix e Iz (ambos corresponden al momento de inercia respecto a un eje perpendicular a la varilla por su centro de inercia), y también vemos que es nulo el momento principal de inercia Iy (pues es nula la distancia al eje y desde cualquier punto de la varilla). |
Se tiene: 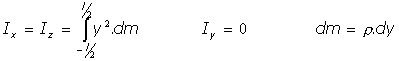
Calculamos:
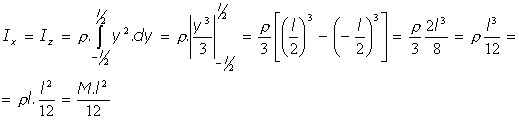
El tensor de inercia diagonalizado es, por consiguiente:
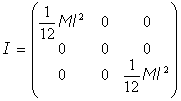
- Momentos principales de inercia de un disco homogéneo de grosor despreciable, masa M y radio R.

|
En este caso, el momento de inercia Iz corresponde al momento de inercia respecto a un eje que atravieza perpendicularmente al disco por su centro de inercia, y los momentos Ix e Iy corresponden al momento de inercia con respecto a un eje diametral, y por tanto, son iguales (Ix=Iy). |
Se tiene:
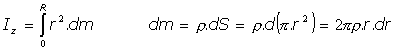
y los momentos diametrales podríamos obtenerlos así:
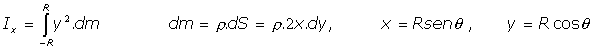
Cálculos:


y, por ser iguales, también será 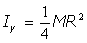
Tensor de inercia diagonalizado:

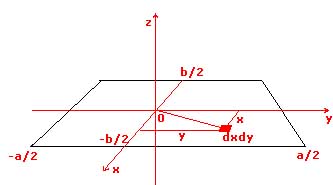
- Momentos principales de inercia de una superficie rectangular, de masa M, base b y altura h, y grosor despreciable.
|
Los momentos de Inercia Ix e Iy son con respecto a un eje contenido en la superficie rectangular, y el momento Iz es con respecto a un eje perpendicular a la superficie por el centro de inercia. |
Se tiene:
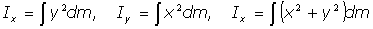
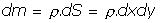
Cálculos:
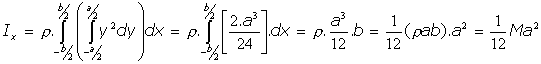
Por analogía es también:
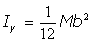
Y también:
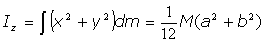
Por lo que el tensor de inercia queda así:

- Momentos principales de inercia de un cilindro homogéneo de masa M, radio R y altura L
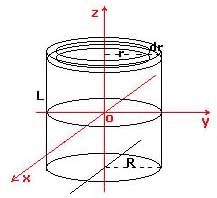
|
El momento de inercia Iz respecto al eje de simetría del cilindro se puede calcular directamente, mientras que los otros dos momentos, iguales, Ix e Iy, pueden calcularse a partir del momento de inercia de un disco con respecto a un eje diametral y aplicando el Teorema de Steiner, se calcula con respecto a un eje paralelo por el centro de masas del cilindro. |
Momento de inercia con respecto al eje de simetría:
Será  con
con 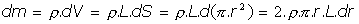

Momentos de inercia respecto a los ejes transversales por el centro de inercia:
El momento de inercia del disco plano de la base del cilindro es, con respecto a un eje diametral:
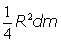 con
con 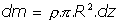
con respecto a un eje paralelo a su diámetro, por ejemplo, el eje x de la figura, se obtiene aplicando el teorema de Steiner:
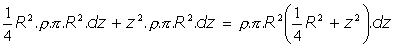
Entonces:
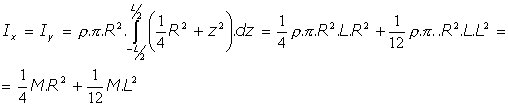
El tensor de inercia, es, por tanto:
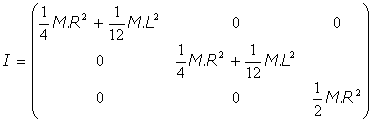
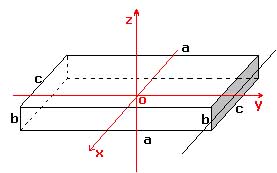
- Momentos principales de inercia de un paralelepípedo de masa M y lados a, b, c.
|
Los tres momentos de inercia han de tener, por razones de simetría, una estructura análoga, y
serian iguales solamente si las tres aristas fueran iguales, es decir, si se tratara de un cubo, o bien
de un paralelepípedo de caras iguales.
Utilizaremos el momento de inercia de una cara rectangular con respecto a un eje contenido en ella
y aplicaremos a continuación el teorema de Steiner
|
El momento de inercia de la cara bc (oscurecida en la figura), es
 con respecto al eje de simetría contenido en
ella que atraviesa el lado b por su punto medio.
Es también
con respecto al eje de simetría contenido en
ella que atraviesa el lado b por su punto medio.
Es también 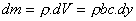 , por lo cual, aplicando Steiner:
, por lo cual, aplicando Steiner:
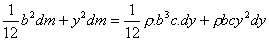
Por tanto, será:
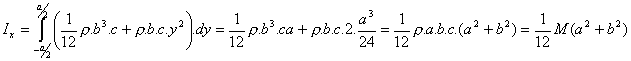
Por analogía, es 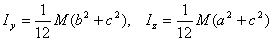
Y el tensor de inercia es
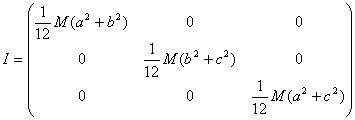
- Momentos principales de inercia de una esfera de masa M y radio R.
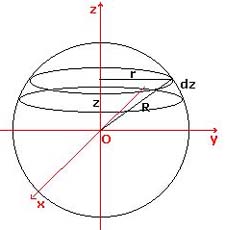
|
Utilizaremos el momento de inercia de un disco plano y sumaremos todos los momentos de inercia de todos los discos paralelos y que son atravesados por un eje principal. Para ello hemos de poner el radio de cada disco elemental en función de la distancia al eje (z en la figura).
Por simetría, es inmediato que los tres momentos principales de inercia de una esfera han de ser iguales.
|
Se tiene entonces que 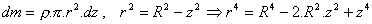
Momento de inercia del disco plano: 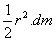
Por tanto, la suma total será:
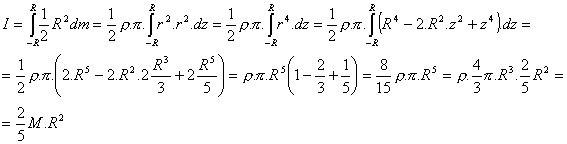
Y son, pues, 
Tensor de inercia:

5. Bibliografía
LANDAU, L.; LIPFSHITZ, E., Curso de Física Teórica, Editorial Mir, Moscu, 1980
FINN, E.; ALONSO,M., Física, Addison-Wesley Iberoamericana, 1995.
TIPLER, Paul A., Física I, Editorial Reverté, Barcelona, 1997
FINZI, Bruno, Mecánica Racional, Urmo, S.A. Ediciones, Bilbao, 1976
Carlos S. CHINEA
casanchi@teleline.es
19 junio 2004
Más artículos de Física

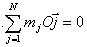
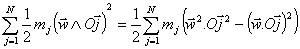
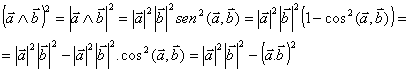
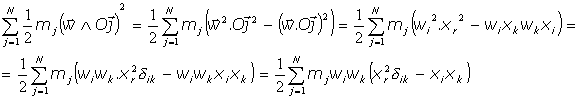
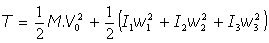
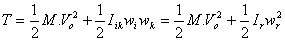
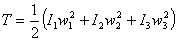
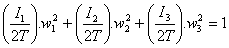
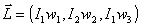

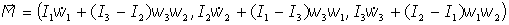

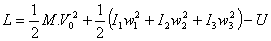

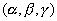 con los ejes de referencia, el
vector unitario en esa dirección tendrá como componentes los cosenos de estos
ángulos y la distancia R de un punto cualquiera del sólido a dicho eje viene dada
por el producto vectorial del vector de posición del punto por dicho vector unitario, por lo que es
con los ejes de referencia, el
vector unitario en esa dirección tendrá como componentes los cosenos de estos
ángulos y la distancia R de un punto cualquiera del sólido a dicho eje viene dada
por el producto vectorial del vector de posición del punto por dicho vector unitario, por lo que es