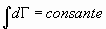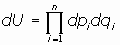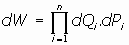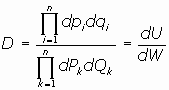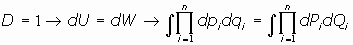01. Introducción:
01.1. Sistemas de partículas:
Un conjunto de partículas con una propiedad común 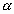 es un
es un 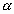 -sistema de partículas.
En realidad, todos los objetos son sistemas de partículas en la mecánica clásica. Un
sistema puede, no obstante, estudiarse, en múltiples aspectos como si fuera una sola
partícula, y esto ocurre en los casos en que la interacción mutua de las partículas del
sistema puede despreciarse en el estudio mecánico de sus peculiaridades dinámicas.
-sistema de partículas.
En realidad, todos los objetos son sistemas de partículas en la mecánica clásica. Un
sistema puede, no obstante, estudiarse, en múltiples aspectos como si fuera una sola
partícula, y esto ocurre en los casos en que la interacción mutua de las partículas del
sistema puede despreciarse en el estudio mecánico de sus peculiaridades dinámicas.
Un sistema de partículas diremos que es cerrado si no sufre interacción desde ningún
sistema exterior, es decir, si consideramos que no está sometido a ningún campo de
interacción externo.
Un sistema se dice conservativo si está exclusivamente sometido a campos externos que
originan fuerzas conservativas, esto es, si existe una función potencial V tal que la fuerza
que sufre el sistema es
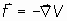
Si el sistema de partículas está sometido además a otras fuerzas no conservativas, que
llamaremos fuerzas disipativas, esto es, no provenientes de una función potencial, tales
como el rozamiento, etc.., diremos que el sistema es no conservativo o bien que es
disipativo.
01.2. Grados de libertad y condiciones de ligadura:
El grado de libertad de cada una de las partículas de un sistema físico puede estar
restringido por condiciones de ligadura, es decir, por condiciones que impiden que todo
el sistema o una parte de él se pueda desplazar libremente en algún sentido. Estas
condiciones pueden ser dependientes del tiempo, y pueden ser representables mediante
ecuaciones matemáticas o ecuaciones diferenciales integrables. o bien, en muchos casos,
solo son representables mediante inecuaciones o sistemas de diferencias.
Un sistema se dice holonomo, o bien, sometido a ligaduras holónomas, si las condiciones
de ligadura son expresables mediante ecuaciones matemáticas entre sus coordenadas o
ecuaciones diferenciales integrables. En caso contrario, se dice que el sistema mecánico
es no holónomo.
Un sistema se dice que es esclerónomo si las condiciones de ligadura son independientes
del tiempo. En caso contrario el sistema se dice que es reónomo o sometido a ligaduras
reónomas.
Por tanto:
Un sistema holonomo esclerónomo es un sistema sometido a condiciones de ligadura
independientes del tiempo expresables mediante relaciones matemáticas entre sus
coordenadas.
Un sistema holónomo reónomo es un sistema sometido a condiciones de ligadura
dependientes del tiempo expresables mediante relaciones matemáticas entre sus
coordenadas.
Un sistema no holónomo esclerónomo es un sistema sometido a condiciones de ligadura
independientes del tiempo no expresables mediante relaciones matemáticas entre sus
coordenadas.
Un sistema no holónomo reónomo es un sistema sometido a condiciones de ligadura
dependientes del tiempo no expresables mediante relaciones matemáticas entre sus
coordenadas.
Los sistemas mas usuales son, naturalmente, los holónomos esclerónomos.
01.3. Coordenadas. Coordenadas generalizadas. El espacio de configuración de
un sistema mecánico:
sea un sistema de N partículas pi, i =1, 2, ..., N. Cada partícula tiene tres
coordenadas en el espacio ordinario, por lo que en total hay 3N coordenadas para el
sistema de partículas.
Si hay k ecuaciones de ligadura entre estas variables se tiene que el número total de
variables independientes es n = 3N - k. Podemos representar por qi ,
i =1,2,...,n a estas
variables independientes, que se denominan coordenadas generalizadas. Sus
correspondientes derivadas temporales se llaman velocidades generalizadas.
Se llama espacio de configuración de un sistema de partículas al espacio cuyos puntos son
las 2n-plas formadas por las coordenadas generalizadas y las velocidades generalizadas
y el tiempo.
Espacio de configuración: 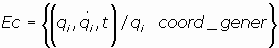
02. El Principio de Mínima Acción:
02.1. El Principio de Hamilton de la Mínima Acción:
En todo sistema de N partículas en donde es 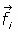 la
fuerza aplicada sobre una partícula de
radio vector
la
fuerza aplicada sobre una partícula de
radio vector 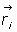 se
verifica que existe siempre una función escalar
se
verifica que existe siempre una función escalar 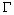 que
llamaremos "energía cinética" del sistema, tal que la integral
que
llamaremos "energía cinética" del sistema, tal que la integral
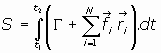
es mínima en el movimiento real del sistema en el espacio de configuración.
A la integral S la llamaremos "acción" del sistema de partículas.
La trayectoria, pues, ha de ser la extremal de la integral definida como acción. O sea, es la
curva para la cual es mínima la acción:
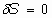
02.2. Expresión matemática de la Acción:
Si la fuerza aplicada a cada partícula,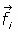 , tiene una
componente conservativa,
, tiene una
componente conservativa, 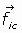 , y otra componente no
conservativa,
, y otra componente no
conservativa, 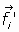 , se tiene que
, se tiene que
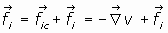
Siendo V una función de las coordenadas generalizadas que llamaremos "energía potencial"
del sistema de partículas. La acción, en definitiva, puede expresarse matemáticamente así:
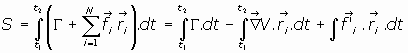
02.3. Ecuaciones de Lagrange:
Aplicando el Principio de Mínima Acción, se tiene:
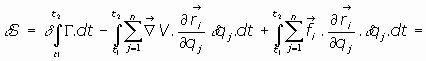
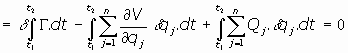
aplicando cálculo variacional a la primera integral (ver ecuaciones variacionales de Euler),
se tiene:
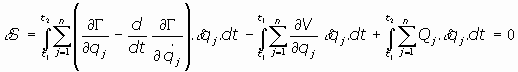
o bien:
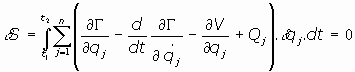
o, lo que es lo mismo:
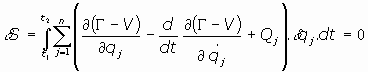
verificándose entonces las n ecuaciones siguientes:
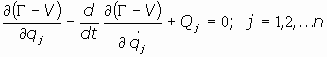
que son las ecuaciones de Lagrange del sistema de partículas. La
función 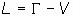 se denomina "lagrangiana" del sistema.
En función de la lagrangiana sería:
se denomina "lagrangiana" del sistema.
En función de la lagrangiana sería:
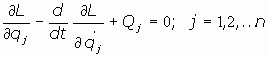
(Ecuaciones de Lagrange)
Para sistemas conservativos es 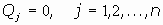 por lo que las ecuaciones anteriores quedan así:
por lo que las ecuaciones anteriores quedan así:
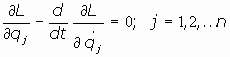
(Ecuaciones de Lagrange para sistemas conservativos)
Para estos sistemas, en donde no existen fuerzas disipativas, la acción del sistema de
partículas es, simplemente, la integral en el tiempo de la función lagrangiana:
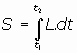
02.4. La lagrangiana:
La lagrangiana de un sistema se define, como ya hemos visto, por la expresión
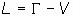 , donde es
, donde es 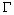 la
energía cinética y V la energía potencial.
la
energía cinética y V la energía potencial.
02.4.1. Determinación:
Toda función L' que difiera de la lagrangiana en la derivada temporal de una función de
las coordenadas generalizadas y del tiempo es, también, lagrangiana del sistema de partículas.
Efectivamente:
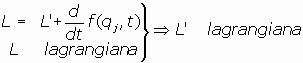
se tiene que si es 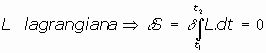
por tanto, es:
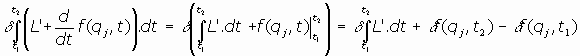
y siendo 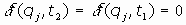 , se
tendrá que
, se
tendrá que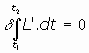 y L' es también lagrangiana.
y L' es también lagrangiana.
02.4.2. Lagrangiana de una partícula libre. La lagrangiana de una particula en un campo
conservativo:
b) El caso de una partícula libre:
La lagrangiana de una partícula libre, al ser una función característica de la misma, no puede
depender de las coordenadas de la partícula ni del tiempo, en virtud de la homogeneidad del
espacio-tiempo. Tendrá que depender solamente de la velocidad, pero en virtud de la isotropía
del espacio, no ha de depender de la dirección de la velocidad, sino, en todo caso de su
módulo, por tanto, ha de poder expresarse en función del cuadrado de la velocidad:
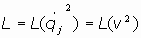
Por otra parte, si consideramos una variación infinitesiamal, u, de la velocidad, se tendría:
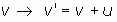
y la lagrangiana también se puede expresar en función de v':
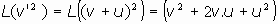
desarrollando en serie y despreciando los términos de órden superior al segundo, se tiene:
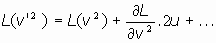
Y siendo lagrangianas tanto 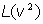 como
como 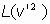 ,
se deduce, en virtud de un resultado expuesto antes,
que el termino restante ha de ser, necesariamente, la derivada temporal de una función de las
coordenadas y del tiempo:
,
se deduce, en virtud de un resultado expuesto antes,
que el termino restante ha de ser, necesariamente, la derivada temporal de una función de las
coordenadas y del tiempo:
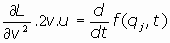
pero esto indicaría que la derivada parcial ha de ser constante, luego:
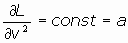
y, en definitiva, es 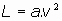 .
.
Llamamos "masa" de la partícula a la constante m = 2.a. Luego, la lagrangina se puede expresar así:
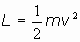
Si se trata de un sistema de N partículas en movimiento libre:
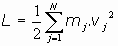
b) Una partícula en un campo exterior de potencial V:
Siendo 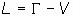 , se tiene que si V= 0 (movimiento libre),
hemos visto que
, se tiene que si V= 0 (movimiento libre),
hemos visto que 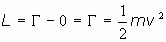 , por tanto, será:
, por tanto, será:
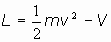
Y si se trata de un sistema de N partículas en movimiento libre, tenemos:
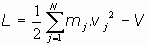
03. Las Ecuaciones de Hamilton:
03.1. Definición de momento lineal:
03.1.1. Momento lineal:
Se define el momento lineal con respecto a la coordenada qj de una partícula de
lagrangina L por
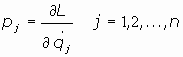
Al n-vector 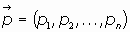 se le llama vector momento lineal o impulso de
la partícula.
se le llama vector momento lineal o impulso de
la partícula.
03.1.2. Coordenadas ignoradas o cíclicas:
Si la lagrangiana L no depende explícitamente de la coordenada qj se dice
que qj es ignorada o cíclica.
Si una determinada coordenada es cíclica, el momento lineal correspondiente es constante, y, al
revés, si el momento es constante, la coordenada correspondiente es cíclica.
Coord qj cíclica 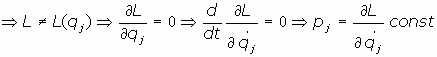
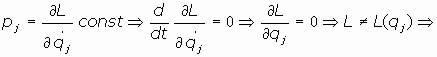 qj ignorada
qj ignorada
03.1.3. Espacio de las fases:
Se define el espacio de las fases de un sistema de partículas como el espacio cuyos puntos son las 2n componentes
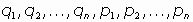
es decir, las coordenadas generalizadas y las correspondientes componentes de momento lineal.
Espacio fases = 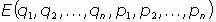
Se define el Corchete de Poisson para dos funciones, f1 y f2, en las
variables del espacio de las fases, y se representa por 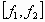 , a
la suma de derivaciones parciales siguiente:
, a
la suma de derivaciones parciales siguiente:
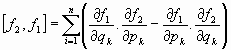
Naturalmente, si una coordenada es ignorada, y como su componente de momento lineal es
constante, el espacio fásico tendría dos componentes menos.
En el caso de que hubiera m coordenadas ignoradas, las dimensiones del espacio de las fases
sería, entonces, 2(n-m).
03.2. La función hamiltoniana:
Se define como hamiltoniana de un sistema de partículas de lagrangiana L a la función
siguiente:
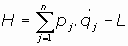
donde las pj son las correspondientes componentes de momento lineal.
03.2.1. Significado:
En un sistema sometido a un campo exterior de potencial V, sabemos que la lagrangiana es de
la forma
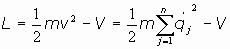
por tanto, se tiene:
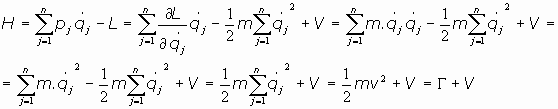
Es decir, la Hamiltoniana de un sistema sometido a un campo exterior constante, no dependiente del tiempo ni de la velocidad, es la energía total del sistema, suma de la energía cinética más la energía potencial.
03.2.2. Invariancia en los sistemas holónomos esclerónomos:
En un sistema holónomo esclerónomo, esto es, en un sistema sometido a condiciones de ligadura independientes del tiempo expresables mediante relaciones matemáticas entre sus coordenadas, su lagrangiana, naturalmente, no depende por tanto expresamente del tiempo, sino, todo lo más, de sus coordenadas y velocidades generalizadas.
Por tanto, al derivar con respecto al tiempo:
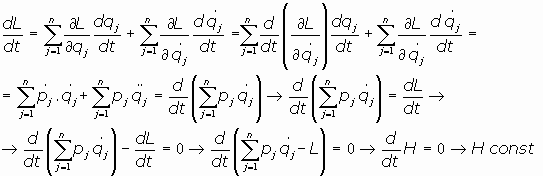
La invariancia de la Hamiltoniana se debe, en definitiva, a la uniformidad del tiempo, al
hecho de que la lagrangiana no depende explicitamente del tiempo en estos sistemas.
Como la Hamiltoniana de un sistema cerrado o sometido a un campo exterior constante es
la energía total del sistema, se deduce, con esto, que la energía total de un sistema
de este tipo es constante.
03.3 Las Ecuaciones de Hamilton:
Haciendo la diferencial de la Hamiltoniana:
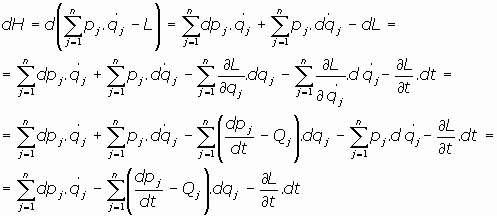
en definitiva, se tiene:
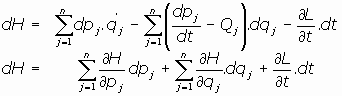
por tanto, al identificar se obtienen un conjunto de ecuaciones que se conocen como
Ecuaciones de Hamilton:
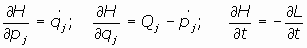
(j=1,2,...,n)
Si se trata de sistemas conservativos:
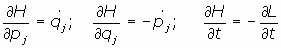
(j=1,2,...,n)
04. Teoremas básicos de la formulación:
04.1. El Teorema de Hamilton-Jacobi:
Para todo sistema sometido exclusivamente a fuerzas conservativas, existe una
ecuación de la forma:
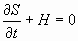
siendo suficiente que tenga una solución completa, S0=S0(qj,pj,t), para
que sean integrables las 2n ecuaciones de Hamilton.
Efectivamente:
Sabemos que si el sistema es conservativo, entonces la acción S es la integral en el tiempo
de la función de Lagrange:
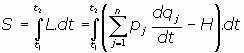
Por tanto, la diferencial dS será:
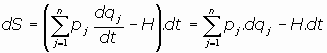
Y por otra parte, al ser la acción S función de las coordenadas generalizadas y del tiempo, se tiene:
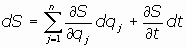
por lo cual, al identificar, tenemos que es:
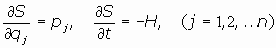
podemos escribir estas relaciones de la forma:
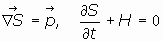
( 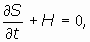 Ecuación de Hamilton-Jacobi)
Ecuación de Hamilton-Jacobi)
Veamos que si existe una función S0=S0(qj,pj,t) que verifica la Ecuación
de Hamilton-Jacobi, entonces existen las integrales de las ecuaciones de Hamilton, es decir
se pueden calcular las integrales siguientes:
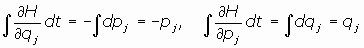
diferenciando la integral S0:
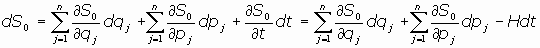
Despejando la H:
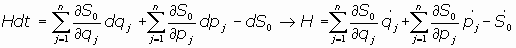
y siendo, por otra parte:
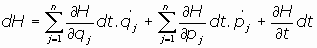
al integrar respecto al tiempo:
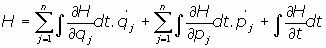
lo que nos permite identificar:
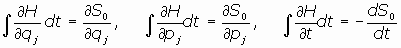
04.2. El Teorema de transformación canónica de variables:
La condición necesaria y suficiente para que una transformación de variables de la forma
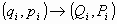
mantenga la invariancia de las ecuaciones de Hamilton
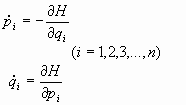
es que exista una función de las coordenadas generalizadas y del
tiempo, 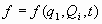 , tal que
, tal que
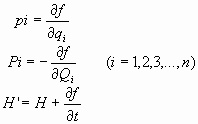
siendo H’ función hamiltoniana del sistema con respecto a las nuevas coordenadas.
Este tipo de transformación se diceTransformación canónica de variables.
En efecto:
- Veamos que es necesaria esa condición si se cumplen las ecuaciones de Hamilton en las
nuevas coordenadas y ímpetus generalizados:
Sea L’ y H’ las funciones de lagrange y Hamilton respecto de las nuevas coordenadas. Se cumple, como ya sabemos, que, para toda función de las coordenadas y del tiempo f(qi, Qi, t) es:
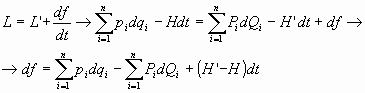
por otra parte:
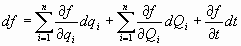
por lo que, identificando:
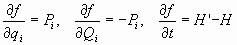
que es la condición indicada y resulta ser, pues, necesario su complimiento.
- Veamos ahora que es suficiente esa condición para que se deduzcan las ecuaciones de
Hamilton en las nuevas coordenadas e ímpetus generalizados:
si se cumplen 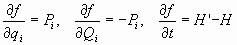 , se tendrá entonces que:
, se tendrá entonces que:
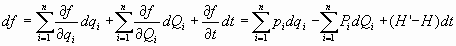
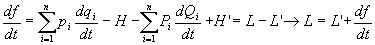
Por tanto las funciones L’ y H’ son respectivamente lagrangiana y hamiltoniana del sistema en
las nuevas variables, cumpliéndose por tanto las ecuaciones de Hamilton:
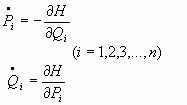
04.3. El Teorema de los Corchetes de Poisson:
La variación temporal de una función 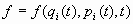 , de las coordenadas e ímpetus generalizados, es
expresable en la forma
, de las coordenadas e ímpetus generalizados, es
expresable en la forma
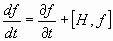
Donde H es la función hamiltoniana del sistema, y [H, f] es el corchete de Poisson de las
funciones H y f.
En efecto:
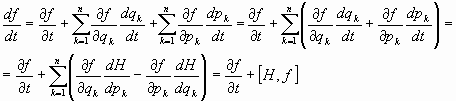
04.4. El teorema del Jacobiano:
El jacobiano de una transformación canónica de variables es siempre igual
a la unidad. O sea:
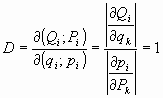
En efecto:
Sea f una función de las coordenadas generalizadas y del tiempo que verifica la condición de la
transformación canónica de variables:
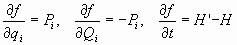
y construyamos una función de la forma 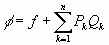 . Se tiene, al diferenciar:
. Se tiene, al diferenciar:
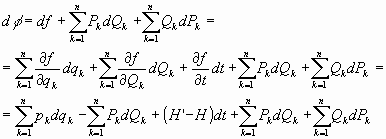
quedando, en definitiva:
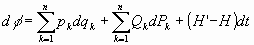
por otra parte, es:
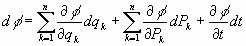
por tanto, al identificar:
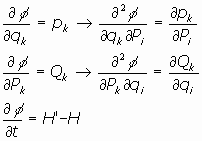
de lo cual:
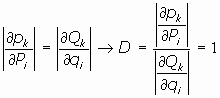
04.5. El Teorema de Liouville:
Dado el espacio de las fases del movimiento real de un a-sistema de partículas con n grados de
libertad, y llamando
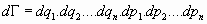
al elemento diferencial de volumen, se verifica que la integral 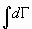 es
invariante con respecto a las transformaciones canónicas de variables. O sea:
es
invariante con respecto a las transformaciones canónicas de variables. O sea:
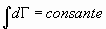
En efecto:
Bastará probar que en una transformación canónica de variables el volumen expresado en unas
variables es el mismo que expresado en las otras.
En las variables (qi, pi): 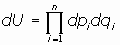
En las variables (Qi, Pi): 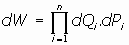
Ahora bien, el jacobiano de la transformación es, precisamente el cociente:
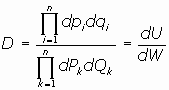
y, por el teorema anterior para el jacobiano:
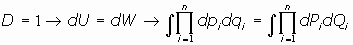
por tanto, se cumple que
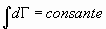
---ooo0ooo---
Carlos
S. Chinea
fisica@casanchi.com
14 septiembre 2002
Otros Artículos de Física






 es un
es un 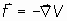
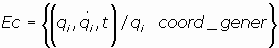
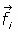 la
fuerza aplicada sobre una partícula de
radio vector
la
fuerza aplicada sobre una partícula de
radio vector 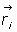 se
verifica que existe siempre una función escalar
se
verifica que existe siempre una función escalar 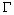 que
llamaremos "energía cinética" del sistema, tal que la integral
que
llamaremos "energía cinética" del sistema, tal que la integral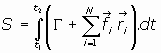
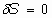
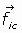 , y otra componente no
conservativa,
, y otra componente no
conservativa, 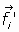 , se tiene que
, se tiene que
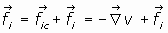
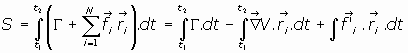
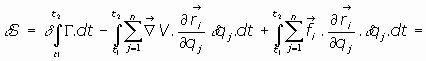
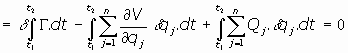
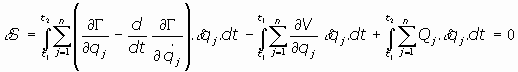
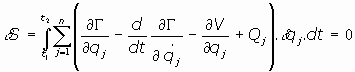
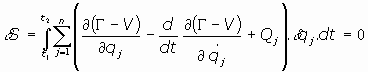
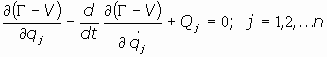
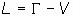 se denomina "lagrangiana" del sistema.
En función de la lagrangiana sería:
se denomina "lagrangiana" del sistema.
En función de la lagrangiana sería:
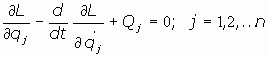
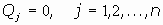 por lo que las ecuaciones anteriores quedan así:
por lo que las ecuaciones anteriores quedan así:
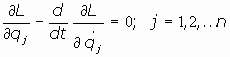
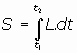
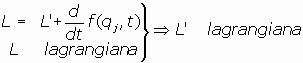
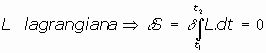
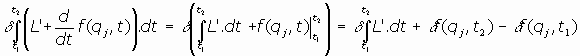
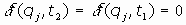 , se
tendrá que
, se
tendrá que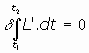 y L' es también lagrangiana.
y L' es también lagrangiana.
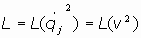
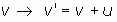
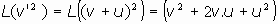
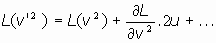
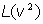 como
como 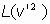 ,
se deduce, en virtud de un resultado expuesto antes,
que el termino restante ha de ser, necesariamente, la derivada temporal de una función de las
coordenadas y del tiempo:
,
se deduce, en virtud de un resultado expuesto antes,
que el termino restante ha de ser, necesariamente, la derivada temporal de una función de las
coordenadas y del tiempo:
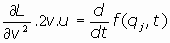
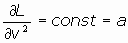
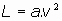 .
.
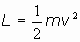
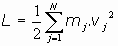
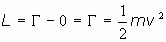 , por tanto, será:
, por tanto, será:
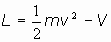
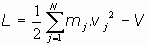
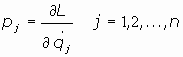
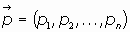 se le llama vector momento lineal o impulso de
la partícula.
se le llama vector momento lineal o impulso de
la partícula.
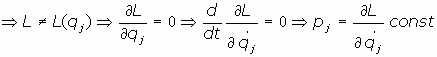
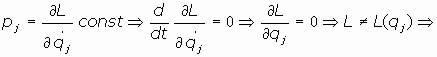 qj ignorada
qj ignorada
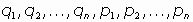
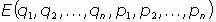
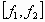 , a
la suma de derivaciones parciales siguiente:
, a
la suma de derivaciones parciales siguiente:
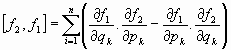
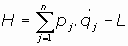
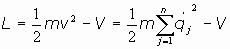
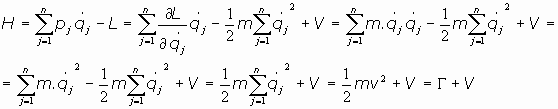
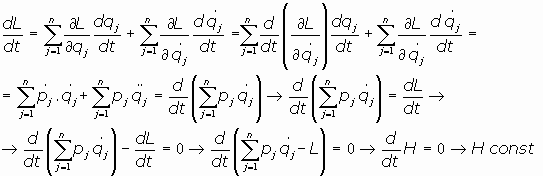
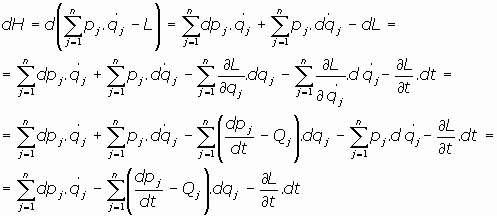
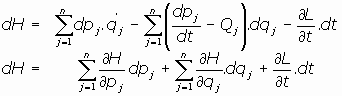
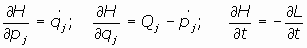
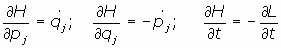
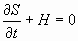
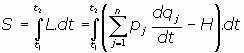
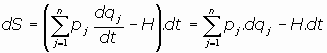
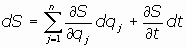
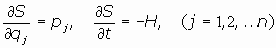
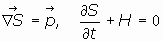
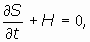 Ecuación de Hamilton-Jacobi)
Ecuación de Hamilton-Jacobi)
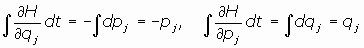
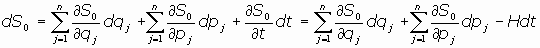
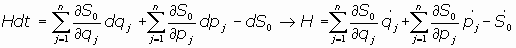
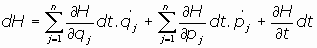
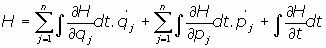
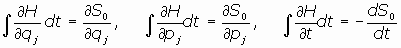
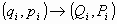
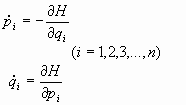
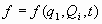 , tal que
, tal que
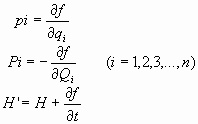
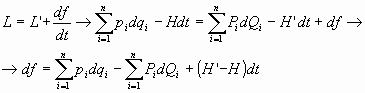
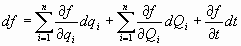
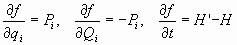
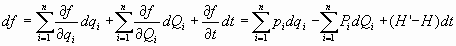
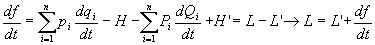
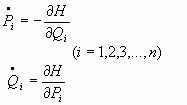
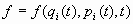 , de las coordenadas e ímpetus generalizados, es
expresable en la forma
, de las coordenadas e ímpetus generalizados, es
expresable en la forma
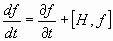
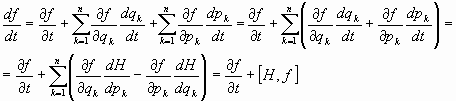
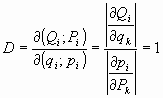
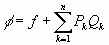 . Se tiene, al diferenciar:
. Se tiene, al diferenciar:
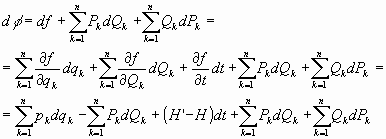
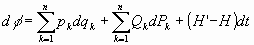
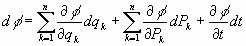
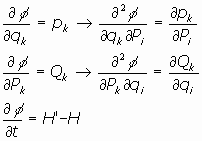
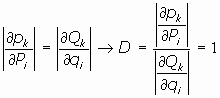
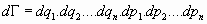
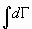 es
invariante con respecto a las transformaciones canónicas de variables. O sea:
es
invariante con respecto a las transformaciones canónicas de variables. O sea: