-----En la Mecánica Clásica podemos considerar campos conservativos, es decir, campos que se derivan de una función potencial V(r). Son, por ejemplo, los casos gravitatorio, electrostático, magnetostático, etc...
Cuando son dos objetos masivos los que interaccionan mediante la generación de campos conservativos, de influencia mutua, se tiene un problema clásico conocido como "Problema de los Dos Cuerpos".
1. Naturaleza del problema:
El problema de los dos cuerpos consiste en el estudio dinámico de dos objetos masivos en el ámbito de su influencia mútua.Sabemos, por ejemplo, que dentro del grupo de galaxias conocido como Grupo Local, donde se encuentra nuestra propia galaxia, la Vía Láctea, hay dos grandes galaxias que tienen, entre ambas, mas del noventa por ciento de la masa total del sistema de las 30 galaxias del grupo: Andrómeda y la Vía Láctea. El centro de Inercia de todo el sistema está, muy aproximadamente, sobre una recta que una a ambas grandes galaxias. La determinación de su posición relativa se puede hacer, con bastante aproximación, resolviendo el problema de Mecánica Clásica No Relativista conocido como Problema de los Dos Cuerpos.
Consideremos, por esquematizar el problema, la existencia de dos partículas de masas m1 y m2, con vectores de posición respecto a un cierto orígen fijo, respectivamente, r1 y r2.
Llamemos también f21 la fuerza que ejerce sobre la particula m1 la partícula m2, y f12 la fuerza que sobre la partícula m2 ejerce la partícula m1. Por principio newtoniano de la mecánica se tiene que f12 = - f21.
2. La situación:
Si llamamos C al centro de inercia de los dos cuerpos, se puede esquematizar la situación mediante la siguiente figura:
3. Relaciones vectoriales:
Se verifican, en definitiva, las siguientes relaciones vectoriales:
y las derivadas del radio vector: 
y podemos considerar la posición relativa de m2 con respecto a m1, asi como, también, la posición relativa de m1 con respecto a m2:
Posición relativa de m2 con respecto a m1:
Posición relativa de m1 con respecto a m2:
Velocidad de m2 con respecto a m1:
Velocidad de m1 con respecto a m2:Por otra parte, se tiene que
Y también se tiene que 
4. La posición de ambas masas con respecto al Centro de Inercia:
Teniendo en cuenta las relaciones vectoriales anteriores, ese obtienen, sin dificultad, los vectores de posición de ambas masas con respecto al Centro de Inercia:
Eliminando rc2:
Eliminando rc1:
Velocidades con respecto al Centro de Inercia:
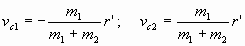
5. La energía total y la Lagrangiana del sistema de las dos masas:
La energía cinética total del sistema formado por los dos cuerpos, de masas m1 y m2, es la energía cinética total considerado como un cuerpo único más la energía cinética interna de la masa m1 en su movimiento relativo con respecto al Centro de Inercia, más la energía cinética interna de la masa m2 en su movimiento relativo con respecto al Centro de Inercia.
y se tiene: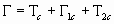 
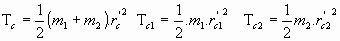
y al sustituir las expresiones del apartado anterior para rc1 y rc2:
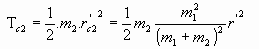
En definitiva, reajustando las sumas:
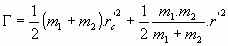
Llamando, "masa reducida del sistema", se tiene la expresión de la función de Lagrange:
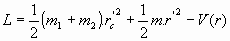
Es decir, la lagrangiana resulta ser una función de las coordenadas r, r' y
:
, quedando ignorada, evidentemente, rc. Por tanto, en virtud de un resultado elemental de la Mecánica Clásica:
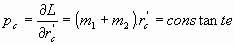
de lo que se deduce que es constante
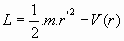
Nos encontramos así que el problema de los dos cuerpos resulta ser equivalente al problema de una partícula de masa m moviéndose en un campo central, del que se derivan fuerzas dirigidas hacia la partícula m1 supuesta fija la partícula m2, o viciversa.
6. Fuerzas:
Las fuerzas que una partícula m sufre en el contexto de un campo central de potencial
pueden ser de atracción o de repulsión:
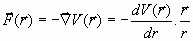
Si
Fuerza de repulsión desde el orígen
Si
Fuerza de atracción hacia el orígen.
7. Trabajo entre dos estados de la trayectoria:
Se tiene, en el movimiento entre dos estados de vectores de posición r1 y r2:
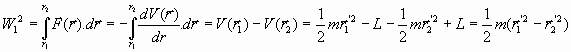
8. Momento angular y forma de la trayectoria:
Veamos, en definitiva, lo que ocurre al desplazarse una partícula de masa m en el contexto de un campo central.
Se tiene, al barrer la particula un ángulo central diferencial:
Sabemos que el momento angular de una partícula en movimiento, con respecto al orígen, es el vector:
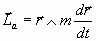
perpendicular, por tanto, a los vectores
y
, es decir, perpendicular a la trayectoria de la partícula.
Si también los vectores
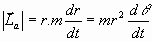
por otra parte, su derivada con respecto al tiempo es:
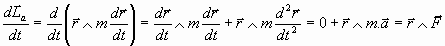
Por ser paralelos los vectores r y
se tiene que es:
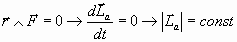
y como es perpendicular a la trayectoria, se deduce que tal trayectoria es plana.
9. Velocidad areolar:
La diferencial del área barrida por la partícula de masa m al desplazarse desde el punto A hasta el punto B es:
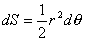
y la velocidad areolar:
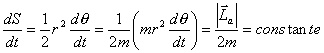
Resulta, en definitiva, que la velocidad con la que barre el área central es constante.
10. Un ejemplo lo tenemos en el sistema Tierra-Sol:
Un ejemplo de sistema de dos cuerpos es, con bastante aproximación, el par constituido por nuestro planeta, La Tierra, y su estrella, el Sol. Podemos hacer el cálculo de la velocidad areolar suponiendo circular la órbita de la Tierra alrededor del Sol:
Velocidad angular:
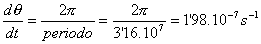
Masa:
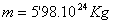
Distancia media al Sol:
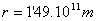
Momento angular:
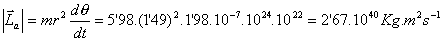
Velocidad de barrido de área:
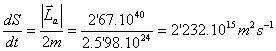
Carlos SÁNCHEZ
CHINEA
casanchi@teleline.es
30 abril 2002
|
|
|
|
